Inducción, Inducción Completa

INDUCCION COMPLETA:

(TEXTO: Extracto editado del libro de Polya: "Cómo plantear y cómo resolver un problema")

La inducción es un modo de razonar que conduce al descubrimiento de leyes generales a partir de la observación de ejemplos particualres y de sus combinaciones. Se emplea en todas las aciencias, aún en las matemáticas, donde se focaliza a la demostración de ciertos tipos de teoremas.realicemos primero una:

INDUCCION SIMPLE

(no como protocolo de demostración)

Casualmente podemos observar que:
1 + 8 + 27 + 64 = 100

Y, constatando que dichos numeros son cubos y su suma un cuadrado, podemos presentar esta observación bajo la forma siguiente:

¿Sucederá siempre que la suma de cubos de números consecutivos sea siempre un cuadrado?

Un científico partiría por tratar de comprobar otros casos, encontrando:

El hecho de que estas diversas sumas de cubos consecutivos sean cuadrados dificilmente puede atribuirse al azar .... Así en primera instancia podríamos decir -por inducción simple: "la suma de los primeros n cubos es un cuadrado .....

Luego la fórmula, la podemos expresar de manera más aprecisa ahora, nuevamente induciendo ....

Pero esta expresión aún es posible simplificarse, porque la suma de la derecha posee una fórmula. Efectivamente es posible disponer una fórmula para:

1+2+3+4+5+6+ .......... + (n-2) + (n-1) + n

Esta fórmula es:

Esta fórmula es fácilmente demostrable y se basa en el mismo tipo de argumentos antes visto en la "Suma de Gauss". Pensemos en la suma que queremos lograr, llamémosla "S":

Escribámosla al revés: Y luego procedamos a sumar ambas sumas S:

Entonces, tras nuestra inducción intuitiva, la gran fórmula que hemos construido es:

Hasta aquí hemos estado pirateando a POLYA !!!!!

Esta es la fórmula que ahora procederemos a DEMOSTRAR por INDUCCION COMPLETA, un protocolo matemático establecido. Nótese que comstruimos la fórmula inductivamente, pero no bajo el protocolo que es conocido como Inducción Matemática y que ahora revisaremos:

INDUCCION COMPLETA
(Como protocolo de demostración)

La Inducción Completa posee un protocolo que resumimos a contiuación:

1) Se verifica si la fórnula se cumple para algunos casos sencillos, los más fáciles, los iniciales.
2) Se supone que se cumple para n.
3) A partir de la aceptación de cumplirse para n, se comprueba que parmanece cierta para el siguiente entero (n+1).

Demostremos entonces el teorema-fórmula anterior:

Hay que demostrar que, para n natural:

Procedamos paso a paso los tres elementos del protocolo anteriomente descrito:

1) Se verifica si la fórnula se cumple para algunos casos sencillos, los más fáciles, los iniciales.
para n = 1

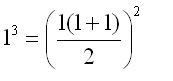Se cumple la fórmula !
para n= 2 Se cumple la fórmula !

2) Se supone que se cumple para n.
Aceptamos entonces que se cumple para n:

3) A partir de la aceptación de cumplirse para n, se comprueba que parmanece cierta para el siguiente entero (n+1).
Sumemos (n+1) al cubo a la fórmula anterior:Fíjense que la fórmula es como si en n hubiésemos reemplazado (n+1) .....

Se CUMPLE para (n+1) !!!!! q.e.d.
- - - - -
Que dice la Enciclopedia Encarta de lo que es la inducción?
Inducción matemática, axioma y a veces método de demostración usando el axioma de inducción. La inducción matemática no debe confundirse con la inducción en otros campos, en donde se define como la técnica de extracción de conclusiones generales a partir de un gran número de casos o experimentos individuales. En matemáticas, esta conclusión, aunque pueda parecer completamente razonable, puede ser falsa. Sin embargo, la inducción matemática se usa a menudo para verificar, o probar, una conjetura obtenida mediante inducción no matemática. Hablando con precisión, el axioma de inducción dice: si M es un conjunto de enteros positivos, con las siguientes propiedades

IA. M contiene al entero 1, y,

IIA. si M contiene al entero n, se puede demostrar que M contiene además al entero n + 1,entonces M contiene a todos los enteros positivos.

La primera parte del axioma de inducción, IA, suele llamarse base, y la segunda parte, IIA, parte inductiva. El axioma de inducción es útil para demostrar ciertas expresiones matemáticas. Suponiendo que la proposición P(n) es verdadera o falsa dependiendo sólo del valor de la n, el axioma de inducción se puede utilizar para demostrar que si

IB. P(1) es verdadera, y

IIB. el saber que P(n) es verdadera, implica que P(n+1) es también verdadera,

entonces P(n) se cumple para cualquier n.

Microsoft ® Encarta ® 2006. © 1993-2005 Microsoft Corporation.

Reservados todos los derechos.