miércoles, 14 de diciembre de 2011
viernes, 9 de diciembre de 2011
lunes, 5 de diciembre de 2011
Treiman Teorema
jueves, 1 de diciembre de 2011
martes, 29 de noviembre de 2011
Geometría NO Euclídea y Relatividad
Geometrías NO Euclídeas y Relatividad
Teorema de Incompletitud de Kurt Godel
viernes, 25 de noviembre de 2011
Simplicidad de la Matemática
"Existe una opinión muy generalizada según la cuál la matemática es la ciencia más difícil cuando en realidad es la más simple de todas. La causa de esta paradoja reside en el hecho de que, precisamente por su simplicidad, los razonamientos matemáticos equivocados quedan a la vista. En una compleja cuestión de política o arte, hay tantos factores en juego y tantos desconocidos o inaparentes, que es muy difícil distinguir lo verdadero de lo falso. El resultado es que cualquier 'tonto'(*) se cree en condiciones de discutir sobre política o arte -y en verdad lo hace- mientras mira la matemática desde una respetuosa distancia",
Ernesro Sábato, "Uno y el Universo", 1945.
(*) la comilla a esta palabra es mía, por considerar que la palabra no es -quizás- la más adecuada.
Razones Trigonométricas - Nemotecnia
poner:
co - ca - co - ca - hip - hip : desplegado de izquierda a derecha y luego, abajo, al revés ....
hip - hip - ca - co - ca - co
agregar rayas fraccionarias .....
co : Cateto Opuesto
ca : Cateto Adyacente
hip : Hipotenusa
Frecuencia
miércoles, 23 de noviembre de 2011
Papomudas - Papomudisure
Las operaciones se hacen en el siguiente orden, de arriba hacia abajo:
PAréntesis
POtencias
MUltiplicaciones
Divisiones
Adiciones
Sustracciones
Nota: en algunos colegios usan PAPOMUDISURE
PAréntesis
POtencias
MUltiplicaciones
DIvisiones
SUmas
REstas
lunes, 14 de noviembre de 2011
Construcción Mecánica
Cuando sólo se emplea Regla y Compás, se llama Construcción Geométrica.
sábado, 12 de noviembre de 2011
Cuándo usar Triángulo de Pascal?
jueves, 10 de noviembre de 2011
domingo, 30 de octubre de 2011
Suma de Gauss
 |
| http://diccio-mates.blogspot.com |
viernes, 21 de octubre de 2011
Cálculo (Rama de las Matemáticas)
El Cálculo es la matemática de los cambios (velocidades, aceleraciones).
También son objeto de cálculo: rectas tangentes, pendientes, áreas, volúmenes, longitudes de arco, centroides, curvaturas y una gran variedad de conceptos que han permitido a científicos, ingenieros y economistas desarrollar modelos para situaciones reales.
Aunque el pre-Cálculo también trata la mayoría de los conceptos antes mencionados, hay una diferencia fundamental entre el pre-cálculo (matemáticas más estáticas) y el cálculo, como una herramienta de con matemáticas más dinámicas. Veamos ejemplos en la siguiente tabla:
Ojo, que esta es la dinámica al interior de las matemáticas:
Tomado de (resumen libre):
Cálculo I - 8ava. Edición.
Autores: Larson - Hostetler - Edwars
Mc Graw Hill
Descartes René - CONTRIBUCION FUNDAMENTAL
¿ Cuál fue la contribución de René descartes ?
" En 1637, el matemático francés René Descartes, revolucionó las matemáticas al unir sus dos ramas principales: el álgebra y la geometría. Con ayuda de un Plano Coordenado de Descartes, los conceptos geométricos se pudieron formular de manera analítica y los algebraicos visualizarse de forma gráfica. La potencia de esta idea es tal, que en 1 siglo se pudo plantear las mayor parte de los elementos del cálculo. "
Tomado de:
Cálculo I
Octava Edicación
Larso - Hostetler - Edwars
Mc Graw Hill
jueves, 20 de octubre de 2011
lunes, 17 de octubre de 2011
Eje de Simetría de Parábola
Nota: Todas las Parábolas tienen Eje de Simetría.
Si las soluciones o raíces de la Ecuación Cuadrática Asociada son x1 y x2, otra forma de
expresar la Ecuación del Eje de Simetría es:
X = (x1+x2)/2
miércoles, 12 de octubre de 2011
Total de Diagonales en un Polígono (Regular o no)
Fórmula:
miércoles, 21 de septiembre de 2011
martes, 20 de septiembre de 2011
Teorema de los Números Primos (de Wikipedia)
Enunciado del teorema
Origami (Tomado de: Construir Matemáticas)
Qué es Origami?
El círculo es la primera figura que ellos aprenden, y con él podemos lograr la realización de hermosos cuentos sin texto para que de vuelo la imaginación de los pequeños, ellos contarán la historia según las imágenes que se muestren.
Es un sistema para introducir la geometría y la matemática, en este nivel aprenden los primeros pasos, reconocen la figura, al plegar pueden reconocer la idea de "mitad o medio", "cuarto", y lograr otras figuras a partir del círculo. El Origami Circular, es un tema muy amplio de creación.
Los niños van adquiriendo motricidad, y entendiendo las consignas en el momento de plegar.
 Pero, con qué se expresa el hecho de plegar papel antes del término "Papiroflexia"? En español, con "hacer pajaritas". De este la palabra "pajarita" no sólo fue aplicada a dar nombre al ave cómica que nosotros conocemos hoy como pajarita, sino también a distintos modelos plegados. Por consiguiente, la palabra "pajarita" en usanza española podría ser referida a cualquiera de los modelos. Vicente Palacios, insiste que dicha palabra "pajarita" se originó en España.
Pero, con qué se expresa el hecho de plegar papel antes del término "Papiroflexia"? En español, con "hacer pajaritas". De este la palabra "pajarita" no sólo fue aplicada a dar nombre al ave cómica que nosotros conocemos hoy como pajarita, sino también a distintos modelos plegados. Por consiguiente, la palabra "pajarita" en usanza española podría ser referida a cualquiera de los modelos. Vicente Palacios, insiste que dicha palabra "pajarita" se originó en España.Números Pentagonales
Aplicación
jueves, 15 de septiembre de 2011
Función Impar
Una función f(x) es impar, si f(x)= - f(-x).
Una funbción se reconoce impar gráficamente, si es simétrica respecto del origen.
Función Par
Una Función f(x) es PAR, si f(x) = f(-x).
Gráficamente se reconoce a una función PAR si es simétrica respecto del eje de ordenadas.
lunes, 29 de agosto de 2011
martes, 23 de agosto de 2011
lunes, 22 de agosto de 2011
Quiralidad
El término quiralidad se refiere a un comportamiento diferenciado de dos entes que son uno simetría especular del otro. El concepto puede aparecer:
- En química, donde la Quiralidad (química) se refiere a una propiedad de las moléculas complejas.
- En física, donde la Quiralidad (física) se refiere a una propiedad de las partículas elementales.
- También en física, donde la Quiralidad (materiales) se refiere a una propiedad de los materiales biisótropos.
- En geometría, donde la Quiralidad (geometría) se refiere a un tipo de simetría.
viernes, 19 de agosto de 2011
miércoles, 17 de agosto de 2011
Demostración Computacional
"En 1976, Kenneth Appel y Wolfgang Haken, afirmaron haber demostrado la conjetura de los cuatro colores. La demostración consistía en una seria de pasos lógicos y analizables uno por uno que llevaban a la conclusión. Y la conclusión era que la conjetura podía quedar reducida a una predicción concerniente a unos 2000 mapas diferentes. Unas 1000 horas de cómputo más tarde, el ordenador concluyo que los dos mil mapas se comportaban de la manera prevista. El teorema era verdadero.
Ciertos matemáticos, como Pierre Deligne, no creen en las demostraciones por ordenador, tan solo creen en las demostraciones claras y que se pueden entender." (Tomado de "El futuro incierto de las demostraciones", de El Rincón del Vago).
martes, 16 de agosto de 2011
Cicloide

Cicloide: Una cicloide es una curva generada por un punto perteneciente a unacircunferencia generatriz al rodar sobre una línea recta directriz, sin deslizarse. (Tomado de Wikipedia)
Georg Pick

George Alexander Pick fué un matemático austriaco nacido en Viena (1859) que murió en un campo de concentración nazi durante la II Guerra Mundial (se cree que en 1943).
G.A.Pick estableció la relación que existe entre los nudos de una malla y la área de un polígono dibujado sobre ella.
Pueden construirse, evidentemente, mallas de muy diversas maneras. Aquí vamos a considerar una malla construída a partir de rectas paralelas y verticales. Cada punto de intersección de una recta horizontal y una vertical se denomina nudo. Un cuadrado de dicha malla será la unidad de superficie.
Teorema de Pick
Teorema de Pick: El matemático austriaco Georg Pick escribió un breve artículo, publicado en 1899, sobre "geometría reticular". De toda una vida de trabajo, en la que trató una amplia variedad de temas, se le recuerda por elcautivador Teorema de Pick.
sábado, 13 de agosto de 2011
Punto Decimal
Ejemplo: en el número 36.9 el punto separa el 36 (la parte entera del número) del 9 (de la parte fraccionaria, 9/10)
jueves, 11 de agosto de 2011
Teorema de Napoleón

Si en un triángulo ABC se construyen triángulos equiláteros exteriores sobre sus lados, los centros de dichos triángulos equiláteros determinan un triángulo equilátero (O1O2 O3) conocido como triángulo de Napoleón exterior.
Analogamente si se construyen sobre los lados del triángulo ABC triángulos equiláteros interiores, sus centros también determinan un triángulo equilátero (P1P2P3) conocido como triángulo de Napoleón interior .
Existe una interesante propiedad que relaciona las áreas de los tres triángulos: El área del triángulo ABC es igual a la diferencia de las áreas de los triángulos de Napoleón exterior e interior .
(Parece ser que Napoleón era aficionado a la Geometría y alguno de los resultados anteriores le ha sido atribuido. En cualquier caso no está muy claro que sus conocimientos geométricos fueran suficientes para llegar a establecer los resultados descritos.)
Texto Tomado de:
http://centros5.pntic.mec.es/Imagen tomada de:
www.edumat.net
martes, 9 de agosto de 2011
lunes, 8 de agosto de 2011
Sección Cónica
Teoría del Caos
Fracción de Unidad
Discreto
Contraejemplo
Base (Sistema Numérico)
Solución Óptima
Iteración
lunes, 1 de agosto de 2011
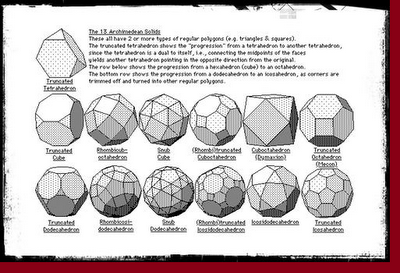
Poliedros Arquimedianos
Espiral de Arquímides
miércoles, 27 de julio de 2011
Cuaterniones (Tomado de Wikipedia)
Los cuaterniones (también llamados cuaternios) son una extensión de los números reales, similar a la de los números complejos. Mientras que los números complejos son una extensión de los reales por la adición de la unidad imaginaria i, tal que i2 = − 1, los cuaterniones son una extensión generada de manera análoga añadiendo las unidades imaginarias: i, j y k a los números reales y tal que i2 = j2 = k2 = ijk = − 1. Esto se puede resumir en esta tabla de multiplicación: la Tabla de Cayley (inglés).
| 1 | i | j | k | |
| 1 | 1 | i | j | k |
| i | i | -1 | k | -j |
| j | j | -k | -1 | i |
| k | k | j | -i | -1 |
1, i, j, k, son entonces las "bases" de las componentes de un cuaternión.
Tipos de Infinito


Número Deficiente
Número Abundante
martes, 26 de julio de 2011
Numerales (Algunos)
Número Algebraico
Números Primos Gemelos
Números Amigos
- Los divisores propios de 220 son 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 y 110, que suman 284.
- Los divisores propios de 284 son 1, 2, 4, 71 y 142, que suman 220.
Aritmética
viernes, 22 de julio de 2011
Módulo de Vector

Composición de Traslaciones
Suma de Vectores (Forma Analítica)
jueves, 21 de julio de 2011
Cocientes Notables

Valor Numérico
miércoles, 20 de julio de 2011
Vector Normal
Vector NORMAL: El vector ![]()
es un vector normal al plano, es decir,
perpendicular al plano.
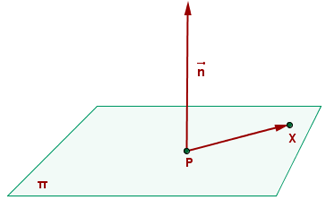
(Tomado de ditutor.com)
Triedro
martes, 19 de julio de 2011
lunes, 4 de julio de 2011
Miembros
miércoles, 29 de junio de 2011
Magnitud
Medir
Polinomio
Polinomio Ordenado
martes, 28 de junio de 2011
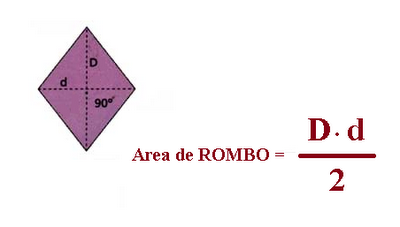
Área de Rombo
Punto Doble
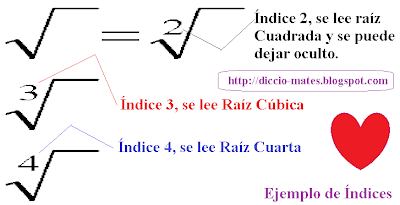
Índice
Escuadra

Escuadra: Instrumento geométrico de construcción, generalmente de forma triangular con un ángulo recto.
Diagrama
lunes, 27 de junio de 2011
Ecuación Dimensional
Geometría Descriptiva
Geometría NO Euclídea
Geometría Euclídea
Teorema de Pasch
Triángulo Esférico Trirrectángulo
Función Trascendental
Función Racional
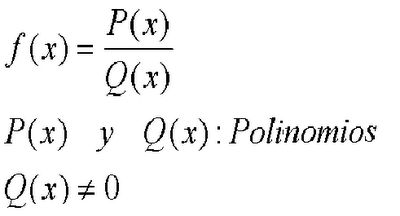
Función Algebraica
Álgebra de Funciones
















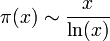 ,donde ln (x) es el
,donde ln (x) es el 












