Coordenadas Cilíndricas

Círculo Unitario y Razones Trigonométricas Ángulos Notables

Orden de Simetría

Orden de Simetría: Número que indica la cantidad de giros necesarios para que el objeto coincida con su posición inicial. Este concepto es referido a la Simetría Rotacional (en este diccionario).

Perímetros y Áreas de Figuras Planas

(Haz doble click en la figura para agrandar)

Raíces de la Función Cuadrática

Raíces de la Función Cuadrática: Corresponden a las soluciones de una ecuación cuadrática.

Sucesos o Eventos

Sucesos o Eventos: Elemento de un espacio muestral de un experimento aleatorio.

Sucesos Combinados

Sucesos Combinados: Dos sucesos pueden ocurrir al mismo tiempo (A y B), puede ocurrir al menos uno de ellos (A o B), o bien, pueden ser excluyentes (no existe la probabilidad de que ocurran ambos sucesos.

Alfabeto Griego

Dilatación y Contracción de una Parábola

Dilatación y Contracción de una Parábola: Se refiere a la abertura de la gráfica de la parábola, cosa que depende del valor del coeficiente numérico de la "x" al cuadrado.

Ecuación Vectorial del Plano

Ecuación Vectorial del Plano: Está determinada por un punto fijo y dos vectores directores, como sigue:

Ecuación Vectorial de la Recta

Ecuación Vectorial de la Recta: Está determinada por un punto fijo y un vector director. Su forma es:

Dominio de una Función

Dominio de una Función: Conjunto de todos los valores que puede tomar la variable independiente.

Recorrido de una Función

Recorrido de una Función: Conjunto de todos los valores que puede tomar la variable dependiente.

Producto Escalar

Producto Escalar: Es el producto del módulo de un vector por la proyección ortogonal de otro vector sobre él. El producto escalar da como resultado un número dado por la expresión:

si ambos vectores están en coordenadas tenemos:

Principio de Euler

Principio de Euler: Relaciona el número de caras, vértices y aristas de un poliedro convexo:

Nº Caras + Nº Vértices = 2 + Nº Aristas

Módulo de Véctor

Módulo de Véctor: Es la longitud del segmento determinado por el vector. Su expresión es, para un véctor como (a1,a2):

Media Aritmética Ponderada

Media Aritmética Ponderada: Es la media de los datos que no poseen la misma ponderación o importancia.

Logaritmo

Logaritmo: El logaritmo en base a de un número x es el exponente y al que hay que elevar la base para obtener dicho número. Es decir,

Kilo

Kilo: Prefijo que significa mil.

Oblícuo

Oblicúo: En declive. No de arriba abajo ni de izquierda a derecha.

Ángulos: no de 90°, 180°, etc.

(Tomado de Disfruta las Matemáticas)

Par Ordenado

Par Ordenado: Dos números escritos en un cierto orden. Usualmente están escritos entre paréntesis, así: (4,5)

Pueden ser usados para mostrar la posición en un gráfico, donde el valor "x" (horizontal) es primero, y el valor "y" (vertical) es el segundo.

aquí el punto (12,5) está 12 unidades a lo largo (Eje Abcisas), y 5 unidades arriba (Eje Ordenadas).

Capicúa

Capicúa = Palíndromo

Algo que se lee igual hacia adelante o hacia atrás.

Ejemplos:

La palabra "madam" es un palíndromo.

La frase "¿Acaso hubo búhos acá?" es un palíndromo (Ignorando los espacios y acentos).

El número "17371" es un palíndromo.

Residuo / Resto

Residuo, Resto: La cantidad que sobra luego de una división (como pasa si un número no puede ser dividido exactamente por otro).

Ejemplo: 19 no puede ser dividido exactamente por 5. Lo más cerca que se puede llegar sin pasarse es 3 x 5 = 15, lo cual es 4 menos que 19.

Entonces la Respuesta de 19 ÷ 5 es 3 con un residuo de 4.

(Tomado de Disfruta las Matemáticas)

Unidad de Medida

Unidad de Medida: Una cantidad usada como estándar de medida.

Ejemplo: Unidades de tiempo son el segundo, minuto, hora, día, semana, mes, año y década.

(Tomado de Disfruta las Matemáticas)

Valor Posicional

Valor Posicional: Es el valor donde se encuentra un dígito en el número, como las unidades, centenas o milésimas. Por ejemplo, en el número 13.432, el valor posicional de 4 es centenas.

Topología

Topología: Estudio de las propiedades de los objetos geométricos que se mantienen cuando los objetos son deformados continuamente, sin romperlos.

(Tomado de Wikipedia:)

La Topología (del griego τόπος, “lugar”, y λόγος, “estudio”) es la rama de las matemáticas dedicada al estudio de aquellas propiedades de los cuerpos geométricos que permanecen inalteradas por transformaciones continuas.¹ Es una disciplina que estudia las propiedades de los espacios topológicos y lasfunciones continuas. La Topología se interesa por conceptos como proximidad, número de agujeros, el tipo de consistencia (o textura) que presenta un objeto, comparar objetos y clasificar, entre otros múltiples atributos donde destacan conectividad, compacidad, metricidad o metrizabilidad, etcétera.

Los matemáticos usan la palabra topología con dos sentidos: informalmente es el sentido arriba especificado, y de manera formal se refieren a una cierta familia de subconjuntos de un conjunto dado, familia que cumple unas reglas sobre la unión y la intersección. Este segundo sentido puede verse desarrollado en el artículo espacio topológico.

Fractal

Fractal (de Wikipedia):

Un fractal es un objeto semigeométrico cuya estructura básica, fragmentada o irregular, se repite a diferentes escalas.¹ El término fue propuesto por el matemático Benoît Mandelbrot en 1975 y deriva del Latín fractus, que significa quebrado o fracturado. Muchas estructuras naturales son de tipo fractal.

A un objeto geométrico fractal se le atribuyen las siguientes características:²

• Es demasiado irregular para ser descrito en términos geométricos tradicionales.
• Posee detalle a cualquier escala de observación.
• Es autosimilar (exacta, aproximada o estadísticamente).
• Su dimensión de Hausdorff-Besicovitch es estrictamente mayor que su dimensión topológica.
• Se define mediante un simple algoritmo recursivo.

No basta con una sola de estas características para definir un fractal. Por ejemplo, la recta real no se considera un fractal, pues a pesar de ser un objeto autosimilar carece del resto de características exigidas.

Un fractal natural es un elemento de la naturaleza que puede ser descrito mediante la geometría fractal. Las nubes, las montañas, el sistema circulatorio, las líneas costeras³ o los copos de nieve son fractales naturales. Esta representación es aproximada, pues las propiedades atribuidas a los objetos fractales ideales, como el detalle infinito, tienen límites en el mundo natural.

Navaja de Ockham

La navaja de Ockham (a veces escrito Occam u Ockam), principio de parsimonia, es un principio filosófico atribuido a Guillermo de Ockham (1280-1349), según el cual cuando dos teorías en igualdad de condiciones tienen las mismas consecuencias, la teoría más simple tiene más probabilidades de ser correcta que la compleja.¹

(Tomado de Wikipedia)

En ciencia, la navaja de Ockham se utiliza como una regla general para guiar a los científicos en el desarrollo de modelos teóricos, más que como un árbitro entre los modelos publicados. En el método científico, la navaja de Occam no se considera un principio irrefutable de la lógica, y ciertamente no es un resultado científico. "La explicación más simple y suficiente es la más probable, mas no necesariamente la verdadera", según el principio de Ockham. En ciertas ocasiones, la opción compleja puede ser la correcta. Su sentido es que a igualdad de condiciones, sean preferidas las teorías más simples. Otra cuestión diferente serán las evidencias que apoyen la teoría. Así pues, de acuerdo con este principio, una teoría más simple pero menos correcta no debería ser preferida a una teoría más compleja pero más correcta.

Qué ha de tenerse en cuenta para medir la simplicidad, sin embargo, es una cuestión ambigua.¹ Quizás la propuesta más conocida sea la que sugirió el mismo Ockham: cuando dos teorías tienen las mismas consecuencias, debe preferirse la teoría que postule la menor cantidad de (tipos de) entidades.² Otra manera de medir la simplicidad, sin embargo, podría ser por el número deaxiomas de la teoría.¹

La teoría de la navaja de Ockham se aplica a casos prácticos y específicos, englobándose dentro de los principios fundamentales de la filosofía de la escuela nominalista que opera sobre conceptos individualizados y casos empíricos.

Hexaedro o Cubo

(De Wikipedia:) Un hexaedro es un poliedro de seis caras. Con este número de caras ha de ser un poliedro convexo, y sus caras han de ser polígonos de cinco lados o menos. Si las seis caras del hexaedro son cuadrados congruentes, el hexaedro se denomina regular (cuerpo frecuentemente conocido comocubo), siendo entonces uno de los llamados sólidos platónicos.

Dodecaedro

(De Wikipedia:) Un dodecaedro es un poliedro de doce caras, convexo o cóncavo. Sus caras han de ser polígonos de once lados o menos. Si las doce caras del dodecaedro son pentágonos regulares, iguales entre sí, el dodecaedro es convexo y se denomina regular, siendo entonces uno de los llamadossólidos platónicos.

Octaedro

(De wikipedia:) Un octaedro es un poliedro de ocho caras. Con este número de caras puede ser un poliedro convexo o un poliedro cóncavo. Sus caras han de serpolígonos de siete lados o menos. Si las ocho caras del octaedro sontriángulos equiláteros, iguales entre sí, el octaedro es convexo y se denomina regular, siendo entonces uno de los llamados sólidos platónicos.

Tetraedro

Tetraedro: 4 caras, 4 vértices, 6 aristas.

(de Wikipedia:) Un tetraedro es un poliedro de cuatro caras. Con este número de caras ha de ser un poliedro convexo, y sus caras triangulares, encontrándose tres de ellas en cada vértice. Si las cuatro caras del tetraedro son triángulos equiláteros, iguales entre sí, el tetraedro se denomina regular. El tetraedro es el símplex tridimensional.

Suficiencia de Datos

EVALUACIÓN DE SUFICIENCIA DE DATOS

(En PSU: INSTRUCCIONES PARA LAS PREGUNTAS Nº 64 A LA Nº 70)

En las preguntas siguientes no se le pide que dé la solución al problema, sino que decida si

los datos proporcionados en el enunciado del problema más los indicados en las

afirmaciones (1) y (2) son suficientes para llegar a esa solución.

Usted deberá marcar la letra:

A) (1) por sí sola, si la afirmación (1) por sí sola es suficiente para responder a la pregunta, pero la afirmación (2) por sí sola no lo es,

B) (2) por sí sola, si la afirmación (2) por sí sola es suficiente para responder a la pregunta, pero la afirmación (1) por sí sola no lo es,

C) Ambas juntas, (1) y (2), si ambas afirmaciones (1) y (2) juntas son suficientes para responder a la pregunta, pero ninguna de las afirmaciones por sí sola es suficiente,

D) Cada una por sí sola, (1) ó (2), si cada una por sí sola es suficiente para responder a la pregunta,

E) Se requiere información adicional, si ambas afirmaciones juntas son insuficientes para responder a la pregunta y se requiere información adicional para llegar a la solución.

Ejemplo: P y Q en conjunto tienen un capital de $ 10.000.000, se puede determinar el

capital de Q si:

(1) Los capitales de P y Q están en razón de 3: 2

(2) P tiene $ 2.000.000 más que Q

A) (1) por sí sola

B) (2) por sí sola

C) Ambas juntas, (1) y (2)

D) Cada una por sí sola, (1) ó (2)

E) Se requiere información adicional

En este ejemplo, usted puede observar que con los datos proporcionados en el enunciado

más los indicados en la condición (1) es posible llegar a la solución, en efecto:

P: Q = 3: 2, luego

(P + Q): Q = 5: 2, de donde

$ 10.000.000: Q = 5: 2

Q = $ 4.000.000

Sin embargo, también es posible resolver el problema con los datos proporcionados en el

enunciado (P + Q = $ 10.000.000) y en la condición (2) (P = Q + $ 2.000.000).

Por lo tanto, usted debe marcar la clave D) Cada una por sí sola, (1) ó (2).

Ángulo de Elevación - Ángulo de Depresión

Ángulos de elevación y de Depresión: Son aquellos formados por la horizontal, considerada a nivel del ojo del observador y la línea de mira, según que el objeto observado esté por sobre o bajo esta última.

(Tomado de Recopilación A. Sánchez)

Icosaedro

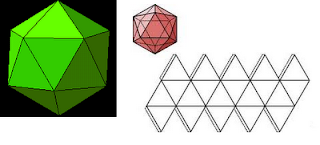
Icosaedro: Poliedro de 20 caras. El icosaedro tiene por caras 20 triángulos equiláteros congruentes.

Isomórfico

Isomórfico: En correspondencia biunívoca.

Suma

Suma: Resultado de la adición de 2 o más cantidades.

Antinomia

Antinomia: Paradoja

Familia

Familia: Conjunto de curvas o figuras relacionadas. Por ejemplo, la curva: y=4x + c, representa una familia de rectas paralelas cuya pendiente es 4.

Variable Aleatoria

Variable Aleatoria: Cada vez que se realiza un experimento aleatorio, se relacionan los eventos a un número, con el fin de representar e interpretar los fenómenos que provoca dicho experimento aleatorio.

Consideremos en experimento de lanzar 3 monedas al aire. Los resultados posibles son:

Podemos establecer una relación entre el espacio muestral w y un número mediante la siguiente regla:

X: número de caras.

X=0, para (SSS)

X=1, para (SSC), (SCS), (CSS)

X=2, para (CCS), (CSC), (SCC)

X=3, para (CCC)

De esta forma se construye el concepto de variable Aleatoria, el cuál corresponde a una regla que relaciona elementos de un espacio muestral con un número. En este caso es el número de caras, que asocia los elementos de "w", con un conjunto de números pertenecientes a los Reales (R).

Matemáticamente, la regla que relaciona los elementos del espacio muestral con un número se define como función (que se denota por X), cuyo dominio son los elementos del espacio muestral y el recorrido de los números reales, es decir:

En el ejemplo anterior se tiene:

X(sss) = 0

X(ssc)=X(scs)=X(css)=1

X(scc)=X(csc)=X(ccs)=2

X(ccc)=3

A nivel de enseñanza media, en Chile, se estudian variables aleatorias, por lo general, discretas. Por tanto la función, la mayoría de las veces va de:

Proporcionalidad en el Círculo

Anillo Circular

Anillo Circular es lo mismo que Corona Circular:

Ángulo Interior

Ángulo Interior:

Congruencia de Triángulos

(Recopilación A. Sánchez)

Ángulo de Inclinación y Pendiente de la Recta

Ángulo de Inclinación y Pendiente:

(Tomado de Recopilación de A. Sánchez)

Problemas con Fracciones

PROBLEMAS CON FRACCIONES:

Son problemas en que se pide calcular la parte de un todo, es decir, una fracción de un

número. La fracción a/b de un número x se calcula multiplicando (a/b) por x.

Sistema Circular

Sistema Circular: Es uno de los sistema de medida de ángulos que existe.

En este sistema de medición la unidad de medida es el radián (rad.). Un radián se define como la medida del ángulo, que enbcierra un arco de circunferencia de longitud igual al radio de ésta. Esto es, dada una circunferencia de radio "r", un radián, es la medida del ángulo que forma un arco de circunferencia cuya longitud es "r".

Luego la circunferencia tiene asociada una longitud de 2 veces Pi (3,1415....) radianes.

(Tomado de CEPECH 2007)

Sistema Centesimal

Sistema Centesimal: Es uno de los tres sistemas de medida de ángulos que existe.

Este sistema divide una circunferencia en 400 partes iguales, su unidad de medida es el grado centesimal o gradián (g), el cual corresponde a una de las 400 partes.

En resumen, en este sistema una circunferencia mide 400º.

Sistema Sexagesimal

Sistema Sexagesimal: En uno de los tres sistemas para medir ángulos.

Este sistema divide a la circunferencia en 360 partes iguales, generando, de esta forma, una división en 360 arcos iguales. A cada uno de los ángulos que se forman uniendo el centro de la circunferencia con los extremos de los respectivos arcos se le asocia como medida un grado sexagesimal (1º), el cual corresponde a una de las 360 partes en que se dividió la circunferencia. cada una de estas 360 partes, se puede a su vez dividir, en 60 partes iguales. Cada una de las divisiones así generadas de un grado sexagesimal se llama minuto (1' ) sexagesimal. A su vez los minutos sexagesimales se dividen en 60 segundos sexagesimales (cada uno de ellos se denota 1").

En resumen, en este sistema, la medida del ángulo que describe la circunferencia es 360º; la de una que describe una semicircunferencia será de 180º y así sucesivamente.

(Tomado de CEPECH 2007)

Posición Relativa de 2 Rectas

Posición Relativa de 2 Rectas:

Posición Relativa de Recta y Plano

Posición relativa de Recta y Plano:

Existencia de Función Inversa - Criterio

Criterio de Existencia de Función Inversa:

Inversa - Estrategia de Búsqueda

Estrategia de Búsqueda de Inversa:

Área Triángulo Rectángulo (Cualquiera)

Área de Triángulo Rectángulo (Cualquiera):

Triángulo de Pascal y Potencias del Binomio (C+S)

(Recopilcaión A. Sánchez)

Pirámide

Pirámide:

Ecuaciones con Fracciones

Ecuaciones con Fracciones: Cuando una ecuación contiene fracciones, puede escribirse en una forma más sencilla si se multiplican ambos miembros de la igualdad por el mínimo común múltiplo de todos los denominadores de la ecuación. De esta forma se obtiene una ecuación que no contenga fracciones.

Resolución Gráfica de Sistema de Ecuaciones

RESOLUCIÓN GRÁFICA de un Sistema de Ecuaciones: Para resolver gráficamente un sistema de dos ecuaciones lineales con dos incógnitas, se representan ambas rectas en un sistema de ejes coordenados, con lo cual surge una de las siguientes posibilidades.

i) Las rectas se intersectan en un punto, cuyas coordenadas (a, b) es la solución del sistema

(figura 1).

ii) Las dos rectas coinciden, dando origen a infinitas soluciones

(figura 2).

iii) Las dos rectas son paralelas (no se intersectan), por lo tanto no hay solución

(figura 3).

Sistemas de Ecuaciones

SISTEMAS DE ECUACIONES

Dos ecuaciones de primer grado, que tienen ambas las mismas dos incógnitas, constituyen

un sistema de ecuaciones lineales.

La forma general de un sistema de ecuaciones de primer grado es:

Ax + By = C

Dx + Ey = F

donde A, B, C, D, E y F son números reales.

Se denomina solución del sistema a todo par (x, y) que satisfaga simultáneamente ambas

ecuaciones.

OBSERVACIÓN: Cada ecuación de un sistema de ecuaciones, representa una línea recta

en un sistema de ejes coordenados.

(Tomado de Recopilación de A. Sánchez)

Análisis Soluciones Sistema Ecuaciones de 2 x 2

(Tomado de Recopilación A. Sánchez)

Función de Primer Grado

Función de Primer Grado:

Función Identidad

Función Identidad:

Triángulos - Propiedades

Triángulos - Propiedades:

Teorema Recíproco del Teorema General de Thales

Teorema Recíproco del Teorema General de Thales:

(Tomado de la recopilación de A. Sánchez)

Teorema General de Thales

Teorema General de Thales:

(Tomado de la recopilación de A. Sánchez)

Teorema Bisectriz Angulo Exterior Triángulo

Teorema de la Bisectriz de un Ángulo Exterior de un Triángulo:

Teorema Bisectriz Angulo Interior Triángulo

Teorema de la Bisectriz de un Ángulo Interior de un Triángulo:

Teorema de la Mediana en un Triángulo

Teorema de la Mediana en un Triángulo:

Sucesión Monótona Creciente

Sucesión Monótona Creciente: Sucesión en la cual un término es inferior o igual al siguiente.

0/0

Factor

Factor: Cada uno de los términos de una multiplicación.

Recíproco

Recíproco: Corresponde al valor inverso de un número, de forma tal que al efectuar el producto de un número y su recíproco, el resultado es uno.

Rectas Convergentes

Rectas Convergentes: Rectas que tienen un punto en común.

(Tomado de Wikipedia)

Número de Mersenne y Número Primo de Nersenne:

Se dice que un número M es un número de Mersenne si es una unidad menor que una potencia de 2. M_n = 2ⁿ − 1.

Un número primo de Mersenne es un número de Mersenne que es primo. Se denominan así en memoria del filósofo del siglo XVII Marin Mersenne quien en su Cognitata Physico-Mathematicarealizó una serie de postulados sobre ellos que sólo pudo refinarse tres siglos después. También compiló una lista de números primos de Mersenne con exponentes menores o iguales a 257, yconjeturó que eran los únicos números primos de esa forma. Su lista sólo resultó ser parcialmente correcta, ya que por error incluyó M₆₇ y M₂₅₇, que son compuestos, y omitió M₆₁, M₈₉, y M₁₀₇, que son primos; y su conjetura se revelaría falsa con el descubrimiento de números primos de Mersenne más grandes. No proporcionó ninguna indicación de cómo dio con esa lista, y su verificación rigurosa sólo se completó más de dos siglos después.

Actualmente (abril de 2011), sólo se conocen 47 números primos de Mersenne, siendo el mayor de ellos M_43.112.609 = 2^43.112.609−1, un número de casi trece millones de cifras. El número primo más grande que se conocía en una fecha dada casi siempre ha sido un número primo de Mersenne: desde que empezó la era electrónica en 1951 siempre ha sido así salvo en 1951 y entre 1989 y 1992.

Ejes de Simetría en Cuadriláteros

Ejes de Simetría en Triángulos

Amplitud del Intervalo

Amplitud del Intervalo: Es la diferencia entre los límites superior e inferior de un intervalo.

Muestra

Muestra: Es un subconjunto de la población, que debe ser representativo y aleatorio.

Diagrama de Barras - Gráfico de Barras.

Diagrama de Barras - Gráfico de Barras : Se utiliza para variables discretas. Los valores de la

variable aparecen, junto con su frecuencia, representados en forma de barras o segmentos,

de longitud proporcional a la dicha frecuencia.

Gráfico de Sectores, Gráfico Pie - Pie

Gráfico de Sectores - Pie - Gráfico Pie: La representación gráfica se hace por medio de un círculo,

dividido en sectores de áreas proporcionales a las frecuencias de la variable.

(Tomado de Recopilación A. Sánchez)

Polígono de Frecuencias

Polígono de Frecuencias: Cada par; Variable/Frecuencia (xi,fi) da origen a un punto del diagrama cartesiano. Al unir dichos puntos por medio de una línea poligonal, se obtiene un polígono de frecuencias.

(Tomado de Recopilación A. Sánchez)

Pictogramas

Pictogramas: Se aplican a las variables de tipo cualitativo y aquellas de tipo cuantitativo que plantean comparaciones. Utilizan para su grafismo representaciones de las variables, de tamaño proporcional a la frecuencia con que aparece cada uno.

(Tomado de Recopilación PSU de A. Sánchez)

Elemento (Conjunto)

Elemento: Un elemento es cualquier objeto o cosa en el conjunto. Se denota por letras minúsculas y al elemento genérico se le designa por "x".

Conjunto

Conjunto: Podemos entender conjunto como colección, grupo de objetos o cosas. Por ejemplo el conjunto formado por los objetos: "2", "cazuela", "z".

Se denotan los conjuntos por letras mayúsculas.

Así en el ejemplo anterior, si llamamos a ese conjunto como Conjunto A, tendremos:

A = {2, cazuela, z}

Fracciones Parciales - Trucos

Coeficiente K - Intervalos de Confianza

Para Construir Intervalos de Confianza y Márgenes de Error.

(Fuente: santillana Cuarto Medio)