Tipos de Funciones

Conjuntos - Operaciones

Producto Cartesiano

Producto Cartesiano:

Dados dos Conjunto A y B se puede formar un Conjunto C que está constituido por todos los pares ordenados (x,y) en que x sea elemento de A e y un elemento de B. Este Conjunto se llama Producto Cartesiano de A y B y se denota por A x B.

En Palabras: A x B = { (x,y) tal que x pertenece a A e y pertenece a B }

En extricta Notación:

Observaciones Respecto al Producto Cartesiano:

Propiedades de las Probabilidades

Se aceptan libros de regalo, obviamente de matemáticas ....

Si Ud. tiene un libro de Matemáticas que NO ocupe, para mi sería un agrado recibirlo de regalo, para ello ruego enviármelo a:

Claudio Escobar Cáceres

Casilla 204, Correo 17

Santiago, Chile.

Muchas Gracias de Antemano ....

A MI ME SIRVEN PARA SEGUIR AYUDANDO A EDUCAR!

Sistema Inecuaciones Lineales Una Incógnita

Inecuaciones Primer Grado con Una Incógnita.

(Tomado de Recopilación A. Sánchez)

Pasos Para Plantear y Resolver una Ecuación

Para resolver un problema debemos seguir los siguientes pasos:

Paso 1: Leer con atención el problema.

Paso 2: Anotar los datos del problema.

Paso 3: Distinguir cuál es la pregunta del problema y representar ese dato desconocido por

un literal (letra).

Paso 4: Con los datos del problema escribir una ecuación.

Paso 5: Resolver la ecuación.

Paso 6: Comprobar si el resultado está de acuerdo con los datos.

Grafo de Proporcionalidad Inversa

El gráfico de una Proporcionalidad INVERSA

corresponde a una

HIPÉRBOLA EQUILATERA!

Recordemos esa imagen:

Simetrías en una Gráfica

Simetrías en una Gráfica:

1) La gráfica de una ecuación en "x" e "y" es simétrica respecto del eje "Y" si al cambiar (x) por (-x) en la ecuación, se obtiene una ecuación equivalente.

2) La gráfica de una ecuación en "x" e "y" es simétrica respecto del eje "X" si al cambiar (y) por (-y) en la ecuación, se obtiene una ecuación equivalente.

3) La gráfica de una ecuación en "x" e "y" es simétrica respecto del origen (0,0) si al cambiar (x) por (-x) y (y) por (-y) en la ecuación, se obtiene una ecuación equivalente.

Ejemplo: Muestre que la siguiente ecuación es simétrica respecto al origen:

Nota: La gráfica de una ecuación en "x" e "y" es simétrica respecto al eje "Y" si cada uno de los términos tiene exponente par (o es una constante). Por ejemplo, esto sucede en la gráfica de:

(Tomado de Larson-Hosteller-Edwars, Cáculo I, Mc Grown-Hills)

Función de Heaviside

Función (Unitaria) de Heaviside:

La Función Escalón de Heaviside, tambien llamada Función Escalón Unitaria, debe su nombre al matemático inglés Oliver Heaviside. Es una función discontinua, cuyo valor es cero para cualquier argumento negativo y 1 para cualquier argumento positivo.




Tiene aplicaciones en ingeniería de control, en funciones del estilo "encendido y apagado. Representa una función que se enciente en un determinado tiempo y queda prendida indefinidamente.

(En algunos casos vale 1 para el argumento cero)

(Mezcla con texto de Wikipedia).

Fracción Decimal

Fracción Decimal: Fracción que tene como denominador una (cualquiera) potencia de 10.

Distancia entre Punto y Recta

Ojo que en el numerador se incluye un Valor Absoluto:

Operatoria Algebraica

OPERATORIA ALGEBRAICA:

ADICIÓN DE POLINOMIOS

Para sumar y/o restar polinomios se aplican todas las reglas de reducción de términos

semejantes y uso de paréntesis.

MULTIPLICACIÓN DE POLINOMIOS

MONOMIO POR MONOMIO:

Se multiplican los coeficientes numéricos entre sí y los factores literales entre sí usando propiedades de potencias. En el caso de multiplicar un monomio por un producto de

monomios se multiplica sólo por uno de ellos. Es decir,

a · (b · c) = (a · b) · c

MONOMIO POR POLINOMIO:

Se multiplica el monomio por cada término del polinomio.

Es decir, a(b + c + d) = ab + ac + ad

POLINOMIO POR POLINOMIO:

Se multiplica cada término del primer polinomio por cada término del segundo polinomio

y se reducen los términos semejantes, si los hay.

(Recopilación de A. Sánchez)

Uso de Paréntesis

USO DE PARÉNTESIS:

En Álgebra los paréntesis se usan para agrupar términos y separar operaciones. Los paréntesis se pueden eliminar de acuerdo a las siguientes reglas:

Si un paréntesis es precedido de un signo +, este se puede eliminar sin variar los signos de los términos que están dentro del paréntesis.

Si un paréntesis es precedido por un signo –, este se puede eliminar cambiando los signos de cada uno de los términos que están al interior del paréntesis.

Si una expresión algebraica tiene términos agrupados entre paréntesis y ellos a su vez se encuentran dentro de otros paréntesis, se deben resolver las operaciones que anteceden a

los paréntesis desde adentro hacia fuera.

Términos Semejantes

TÉRMINOS SEMEJANTES:

Son aquellos que tienen idéntico factor literal, es decir tienen las mismas letras, y los mismos exponentes, sólo pueden diferir en el coeficiente numérico.

Evaluar una Expresión Algebraica

EVALUACIÓN DE EXPRESIONES ALGEBRAICAS:

Evaluar una expresión algebraica consiste en sustituir las letras por los valores numéricos

dados para luego realizar las operaciones indicadas. Esta sustitución va siempre entre

paréntesis.

Signos de una Potencia

Potencias

Cero elevado a Cero

Cero elevado a Cero: NO está definido.

Tipos de Decimales

(Tomado de la Recopilación del profesor A. Sánchez)

Operatoria con Números Decimales

OPERATORIA CON NÚMEROS DECIMALES:

1. Adición o sustracción de números decimales: Para sumar o restar números decimales

se ubican las cantidades enteras bajo las enteras, las comas bajo las comas, la parte decimal

bajo la decimal y a continuación se realiza la operatoria respectiva.

Así por Ejemplo:

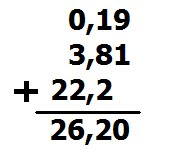
2. Multiplicación de números decimales: Para multiplicar dos o más números decimales,

se multiplican como si fueran números enteros, ubicando la coma en el resultado final, de

derecha a izquierda, tantos lugares decimales como decimales tengan los números en

conjunto.

Así por Ejemplo:

3. División de números decimales: Para dividir números decimales, se puede transformar

el dividendo y el divisor en números enteros amplificando por una potencia en base 10.

Así por Ejemplo:

2,24: 1,2 se amplifica por 100 (dividendo y divisor)

224: 120 y se dividen como números enteros.

Relación de Orden en Q

OBSERVACIONES

1. Para comparar números racionales, también se pueden utilizar los siguientes procedimientos:

a) Igualar numeradores.

b) Igualar denominadores.

c) Convertir a número decimal.

2. Entre dos números racionales cualesquiera hay infinitos números racionales.

(Tomado de Recopilación del profesor A. Sánchez)

Inverso Aditivo de un Racional

Dado Honesto, Moneda Honesta

Dado Honesto: Dado NO cargado, es decir, homogéneo. Donde cada uno de los 6 números tiene casi idéntica probabilidad de salir.

Moneda Honesta: Moneda NO cargada, es decir, homogénea. Donde cada una de los dos posibilidades (cara o sello) tiene igual probabilidad de salir.

Angulo entre 2 rectas con pendiente m1 y m2

Operatoria con Números Complejos

Función Polinómica

Función Polinómica:

Es una función de la forma:

donde "n" es un entero NO negativo y a0, a1, a2, ......, an, son constantes Reales (con "an" distinto de cero). El coeficiente "an", se denomina primer coeficiente y el valor de "n" es el grado de la función polinómica.

El mayor dominio posible de f(x) es R, los Reales.

Fórmulas que Incluyen Complejo Conjugado

Funciones Trigonométricas en Círculo Unidad

Grado a Radián - Radián a Grado

Para comprobar:

23º corresponden a 23/360 = x/2Pi ...... x = 0,401

Pi/6 corresponden a x/360 = (Pi/6)/(2Pi) ...... x = 30º

Racionales

Proporción

Proporción : Igualdad de 2 razones.

Razón

Razón: Relación (división) entre dos cantidades homogéneas.

a/b ;

2/3 ;

3 caballos / 4 caballos ;

son tres ejemplos de Razones.

Romboide

Ventajas de Grafos

Ventajas de Grafos:

Gráfico de Barras: Sirven para comprar frecuencias de valores.

Pictogramas: Se recomienda para representar variables cualitativas, por ejemplo: ciudad de origen.

Gráfico Circular o de Sectores: Es recomendable para representar porcentajes. Para construirlo se divide el círculo en sectores circulares proporcionales a la frecuencia que se quiere representar.

Histograma: Se recomienda para representar datos agrupados. Se compone de líneas contiguas, en la cual cada una representa a un intervalo.

(Tomado de Libro Santillana 8avo. Básico)

Radio

Radio: Segmento que une cualquier punto de una circunferencia con el centro.

Diámetro

Diámetro: Cuerda que une dos puntos de una circunferencia pasando por el centro. En toda circunferencia la medida del diámetro es el doble de la del radio.

Tangente a una Circunferencia

Tangente a una Circunferencia: Recta que tiene sólo un punto en común con una circunferencia.

Secante a una Circunferencia

Secante a una Circunferencia: es una recta que corta a una circunferencia en dos puntos.

Frecuencia Relativa Acumulada

Frecuencia Relativa Acumulada: en la categoría i, es la probabilidad de observar un valor menor o igual al mayor valor que toma la variable en estudio en ese intervalo.

Frecuencia Absoluta Acumulada

Frecuencia Absoluta Acumulada: en el intervalo i es la suma de las frecuencias absolutas observadas hasta el intervalo i.

Frecuencia Relativa

Frecuencia Relativa: Cociente entre la frecuencia absoluta de una variable y el número total de observaciones. La suma de las frecuencias relativas es igual a 1 (o a 100 % en caso de que se expresen porcentualmente).

La frecuencia relativa de la categoría i corresponde a la probabilidad de pertenecer a esa categoría.

Frecuencia Absoluta

Frecuencia Absoluta: Número de veces que aparece cada valor de una variable. La suma de todas las frecuencias absolutas da el tamaño de la población.

Teoremas Relativos a Triángulos Isósceles

Teoremas Relativos a Triángulos Isósceles:

1) Los ángulos basales de un triángulo Isósceles son congruentes.

2) Recíproco del anterior: Si un triángulo tiene dos ángulos de igual medida es Isósceles.

3) La altura trazada desde el vértice de un triángulo isósceles dimidia a la base y bisecta al ángulo del vértice.

4) La transversal de gravedad correspondiente al vértice de un triángulo isósceles, es perpendicular a la base y bisecta al ángulo del vértice.

5) La bisectriz del ángulo del vértice de un triángulo Isósceles, dimidia a la base y perpendicular a ella.

6) Corolario de los anteriores: En un triángulo Isósceles coinciden la altura, la transversal de gravedad y la bisectriz del ángulo de vértice.

7) Las alturas trazadas desde los vértices basales de un triángulo Isósceles tienen la misma medida.

8) Las transversales de gravedad correspondientes a los vértices basales de un triángulo isósceles, tienen la misma medida.

9) Las bisectrices de los ángulos basales de un triángulo isósceles son congruentes.

Teoremas Sobre Polígonos

Teoremas Básicos de Polígonos:

1) Si un polígono tiene "n" lados, la suma de las medidas de los ángulos interiores es: 180º(n-2).

2) Corolario del anterior: Si el polígono es regular de "n" lados tiene "n" ángulos iguales y, por tanto, cada ángulo de un polígono regular mide:

3) La suma de los ángulos exteriores de un polígono es 360º.

Raíces

(Tomado de la Recopilación de A. Sánchez)

Tanto Por Ciento

Operatoria en Q

Adición y Substracción de Números Racionales (Q):

Multiplicación y División de Números Racionales (Q):

Igualdad Entre Números Racionales

Números Racionales (Conjunto Q)

Conjunto Z (Números Enteros)

(Tomado de la Recopilación de A. Sánchez)

Múltiplo y Divisor

MÚLTIPLO Y DIVISOR:

En la expresión a = b · c en que a, b y c son números enteros,

a es múltiplo de b y de c

o bien b y c son divisores o factores de a.

Números Primos, Compuestos y Descomposición en Factores

NÚMEROS PRIMOS, COMPUESTOS Y DESCOMPOSICIÓN EN FACTORES

Números primos: Son aquellos enteros positivos que tienen sólo dos divisores distintos.

Los primeros números primos son: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, …

Números compuestos: Son todos los enteros positivos mayores que uno que no son

primos. Los primeros números compuestos son: 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, …

TEOREMA FUNDAMENTAL de la ARITMETICA:

Todo número compuesto se puede expresar de manera única como el producto de factores de números primos.

Operatoria en Z

OPERATORIA EN Z

ADICIÓN

i) Al sumar números de igual signo, se suman los valores absolutos de ellos conservando

el signo común.

ii) Al sumar dos números de distinto signo, al de mayor valor absoluto se le resta el de

menor valor absoluto y al resultado se le agrega el signo del mayor valor absoluto.

MULTIPLICACIÓN

i) Si se multiplican dos números de igual signo al resultado es siempre positivo.

ii) Si se multiplican dos números de distinto signo el resultado es siempre negativo.

OBSERVACIÓN: La división cumple con las reglas de signos de la multiplicación.

Algoritmo de la División

Trisecar

Trisecar: Cortar un objeto en tres partes iguales.

Por ejemplo, trisecar un segmento de línea significa cortarlo en tres segmentos de línea iguales. Trisecar un ángulo significa dividirlo en tres ángulos iguales.

(Tomado de Diccionario Visual)

Vector

Vector: Segmento orientado que va desde un punto A, punto de origen, a otro punto B, punto extremo.

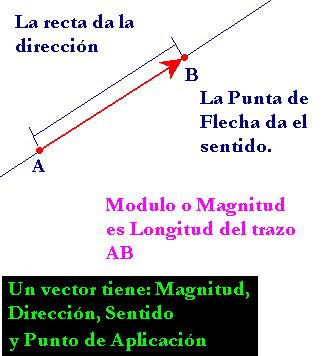
El vector posee dirección, que está dada por la recta que lo contiene o por cualquier recta paralela a ella. El sentido del vector es que que va desde el origen A al extremo B. El módulo o magnitud del vector es la longitud del segmento.

Cantor Georg (1845-1918)

Cantor Georg (1845-1918): Matemático alemán. Catedrático de matemáticas en la Universidad de Halle. Fue el fundador del Congreso Internacional de Matemáticos. Creador de las teorías de Conjuntos y de los números transfinitos, su obra dio lugar a un cambio total en las perspectivas de estudio de las matemáticas y obligó a efectuar un nuevo examen crítico de sus fundamentos. Sus trabajos suscitaron numerosa discusuiones matemático-filosóficas, que lo enfrentaron a la mayoría de los matemáticos de la época.

Biometría

Biometría: Rama de las matemáticas que estudia estadísticamente los fenómenos biológicos.

Bi

Bi: Prefijo griego que significa dos o doble. Ejemplo: Binomio = dos monomios.

Alícuota

Alícuota: Parte que divide exactamente a un todo. Por ejemplo, 4 es una parte alícuota de 8.

Abertura

Abertura: Magnitud o medida de un ángulo, Ejemplo: el ángulo recto tiene una abertura de 90º (en grados sexagesimales)

Equiángulo

Equiángulo: Polígono o cuerpo cuyos ángulos son iguales. Ejemplo: El triángulo Equilátero es equiángulo.

Quebrado

Quebrado: Término con el que se designa también a una fracción.

Euler Leonhard (1707-1783)

Euler Leonhard (1707 - 1783) : Matemático suizo y profesor de la Academia de Ciencias de S. Petesburgo. Formuló el cálculo de variaciones y escribió los primeros tratados completos sobre cálculo diferencial e integral. Su nombre se asocia a una gran cantidad de conceptos matemáticos.

Unicidad

Unicidad: Resultado de las operaciones que se determina sin ambiguedad. Ej.: En el producto 3 x 7 = 21 siempre se dará este resultado (único), cualesquiera sean los conjuntos empleados.

Segmento (Trazo)

Segmento: Parte de una recta, comprendida entre dos extremos que se escojan. se le designa como se muestra a continuación (es decir tiene 2 designaciones).

Número Positivo

Número Positivo: Número Mayor que Cero.

Vector Fijo

Vector Fijo: Vector que tiene un único punto de aplicación.

Contorno

Contorno: Conjunto de líneas que conforman los límites de una figura. Sobre el contorno de una figura se puede medir el perímetro.

Despejar

Despejar: Proceso que consiste en modificar una ecuación, inecuación o sistema hasta que la incógnita quede en uno de los dos miembros de la igualdad (o desigualdad). Mientras en las ecuaciones de primer grado es sencillo despejar la incógnita, en las de segundo grado hay que recurrir a una fórmula, que se complica enormemente cuando son de tercer o cuarto grado. En otras ecuaciones, como las exponenciales, las logarítmicas y las trigonométricas, los métodos que se emplean son distintos y de mayor dificultad.

Hexágono

Hexágono: Polígono formado por 6 lados y 6 ángulos. Cuando sus lados y ángulos son iguales se conoce con el nombre de hexágono regular.

Lados Adyacentes (en Polígono)

Lados Adyacentes (en Polígono): Par de lados que tienen un vértice en común.

Teoremas Básicos del Triángulo

Teoremas Básicos del Triángulo:

1) La suma de las medidas de los ángulos interiores de un triángulo es 180º.

2) La medida del ángulo exterior en un vértice de un triángulo es igual a la suma de las medidas de los dos ángulos interiores no adyacentes con él.

3) Los ángulos exteriores de un triángulo suma 360º.

Veamos en el mismo orden las imágenes de estos tres teoremas:

Operación Algebraica

Operación Algebraica: Operaciones matemáticas (sumar, multiplicar, sacar raíces, etc.) que se realizan a ambos lados de la ecuación o desigualdad.

Binomio

Binomio: Suma de dos Monomios.

Polígono

Polígono: Región del plano delimitada por segmentos de rectas.

Directriz de Parábola

Directriz de Parábola: Es una recta que se usa en la construcción de una parábola como lugar geométrico.

Parábola: Lugar geométrico de todos los puntos del plano tales que su distancia a una recta dada llamada DIRECTRIZ es igual a su distancia a un punto llamado foco.

Análisis Gráfico

Análisis Gráfico: procedimiento usado para graficar en un plano de coordenadas la región solución de un sistema de desigualdades.

Función Raíz Cúbica

Función Raíz Cúbica: se representa por la función anterior y los valores de f(x) están dados según los valores de x. Si:

(Texto Tomado de Santillana 3ro. Medio)

(Gráfico hecho con GRAPHMATICA)

Parábola como Lugar Geométrico

Parábola como Lugar Geométrico: Gráfica de todos los puntos que están a igual distancia de un punto fijo (foco) y una recta (directriz).

Espacio Muestral Equiprobable

Espacio Muestral Equiprobable: Espacio en donde todos los sucesos pertenecientes al espacio muestral, tienen igual probabilidad.

Desigualdad

Desigualdad: Expresión matemática que sirve para representar que cierta cantidad es menor o mayor que otra.

Combinación

Combinación: Selección de cierta cantidad de elementos u objetos de un total.

Sistema Inecuaciones Lineales

Sistema Inecuaciones Lineales: Conjunto de dos o más inecuaciones de una o más incógnitas, cuyas soluciones satisfacen el sistema.

Conjunto Vacío

Conjunto Vacío: Conjunto que NO posee elementos.

Reducción al Absurdo

Reducción al Absurdo: Tipo de demostración que conviene en admitir como cierta la negación de la proposición original para que, llegando a una contradicción sólo sea aceptable la proposición original o tésis.

Basic

Basic: Lenguaje de computación. Uno de los lenguajes más usados.

de Wikipedia:

En la programación de computadoras, el BASIC, siglas de Beginner's All-purpose SymbolicInstruction Code, es una familia de lenguajes de programación de alto nivel. El BASIC original, el Dartmouth BASIC, fue diseñado en 1964 por John George Kemeny y Thomas Eugene Kurtz en el Dartmouth College en New Hampshire, USA, como un medio para facilitar programar computadores a estudiantes (y profesores) que no fueran de ciencias. En ese tiempo, casi todo el uso de los computadores requería codificar software hecho a la medida, lo cual era algo bastante restringido a personas con formación como científicos ymatemáticos. BASIC originalmente fue desarrollado como una herramienta de enseñanza. El lenguaje y sus variantes llegaron a estar ampliamente disponibles en los microcomputadoresa finales de los años 1970 y en los años 1980. El BASIC sigue siendo popular hasta el día de hoy en un puñado de dialectos altamente modificados, y en nuevos lenguajes, influenciados por BASIC tales como Microsoft Visual Basic. Por el año 2006, el 59% de los desarrolladores para la plataforma .NET usaban Visual Basic .NET como su único lenguaje.

Contar

Contar: Procedimiento que hace corresponder a cada elemento de un conjunto, del cual se quiere conocer su cardinalidad, otro conjunto que se toma como referencia (el de los números naturales).

Fórmula de Euler

Fórmula de Euler: Fórmula que relaciona las funciones trigonométricas con la función exponencial.

Hecto

Hecto: Prefijo que expresa a cien.

Lúnula

Lúnula: Porción de esfera limitada por dos circunferencias máximas.

Mega

Mega: Prefijo cuyo significado en un millón.

Oblicuángulo

Oblicuángulo: Triángulo sin ángulo recto. Son oblicuángulos los triángulos acutángulos y obtusángulos.

Punto

Punto: Concepto Matemático-Geométrico no definible. Es por esto que se le conoce como un concepto "primitivo".

Concepto intuitivo que puede entenderse como la intersección de dos rectas o de tres planos.

Región Cóncava

Región Cóncava: Región para la cual dos puntos cualesquiera de ella, al ser unidos por un segmento de recta, algunos (al menos uno) de los puntos del segmento quedan situados fuera de la región.

Región Convexa

Región Convexa: Regió para la cual dos puntos cualesquiera (de la misma) pueden ser unidos por un segmento de recta, quedando todos los puntos del segmento al interior de la región.

Toro

Toro: Superficie generada por una circunferencia que gira al rededor de un eje que es exterior a la curva.

Tripleta Pitagórica

Ver "Terna Pitagórica", en este mismo diccionario.

Vector Cero

Vector Cero: Vector de longitud cero. Vector de valor absoluto cero.

Vigesimal

Vigesimal: Referido al Sistema de Numeración en base 20. También puede representar un conjunto de 20 unidades.

X

X:

1) Letra que simboliza al número 10, en numeración Romana.

2) Letra que se usa para representar al eje de las abcisas, en el sistema de referencia de Coordenadas Cartesianas.

3) Letra que se usa en álgebra para representar incógnitas, en ecuaciones.

4) Letra que se usa en funciones para representar a la variable independiente.

Zona

Zona: Porción de plano o de superficie esférica.

Catetos

Catetos: Cada uno de los lados que forman el ángulo recto en un triángulo rectángulo.

Factorizaciones (Algunas de ellas)