 o los números naturales
o los números naturales  , es decir, se trata de ecuaciones cuyas soluciones son números enteros.
, es decir, se trata de ecuaciones cuyas soluciones son números enteros.Un ejemplo de ecuación diofántica es: 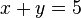
Esta ecuación tiene infinitas soluciones en los números reales. Como regla general, sin embargo, las ecuaciones que aparecen en los problemas tienen restricciones que nos ayudan a limitarnos a un pequeño número de casos e incluso a una única solución.
Por ejemplo, en nuestra ecuación, si restringimos los posibles valores de x e y a los enteros positivos, tenemos 4 soluciones para (x,y):
- (1,4) (2,3) (3,2) (4,1).
Un problema matemático muy famoso que se resuelve por medio de ecuaciones diofánticas es el del mono y los cocos.
Un caso Particular de Ecuación Diofántica: Ecuación pitagórica
Se llama ecuación pitagórica a la ecuación 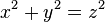 con
con  . Cualquier terna (x, y, z) solución de la ecuación anterior se conoce como terna pitagórica. Además si (x, y, z) es una terna pitagórica solución de la ecuación pitagórica también lo serán:
. Cualquier terna (x, y, z) solución de la ecuación anterior se conoce como terna pitagórica. Además si (x, y, z) es una terna pitagórica solución de la ecuación pitagórica también lo serán:
- La terna alternando x e y: (y, x, z).
- Una terna múltiplo (ky, kx, kz).
- Una terna con algún signo cambiado (-x, y, z), (x, -y, z) o (y, x, -z)
- Cualquier otra terna obtenida mediante una combinación de los procedimientos anteriores.
Se dice que una terna es primitiva, si el máximo común divisor de x, y, z es la unidad, es decir, mcd(x,y,z) = 1. En toda terna primitiva al menos uno de los números x o y es par y z es impar. Puede verse que en esas condiciones todas las ternas primitivas que son de la ecuación pitagórica son de la forma:


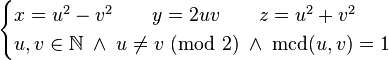

No hay comentarios:
Publicar un comentario