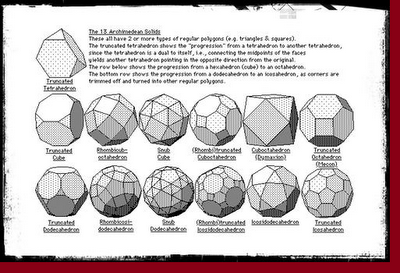
Constantes Matemáticas:

El término quiralidad se refiere a un comportamiento diferenciado de dos entes que son uno simetría especular del otro. El concepto puede aparecer:
"En 1976, Kenneth Appel y Wolfgang Haken, afirmaron haber demostrado la conjetura de los cuatro colores. La demostración consistía en una seria de pasos lógicos y analizables uno por uno que llevaban a la conclusión. Y la conclusión era que la conjetura podía quedar reducida a una predicción concerniente a unos 2000 mapas diferentes. Unas 1000 horas de cómputo más tarde, el ordenador concluyo que los dos mil mapas se comportaban de la manera prevista. El teorema era verdadero.
Ciertos matemáticos, como Pierre Deligne, no creen en las demostraciones por ordenador, tan solo creen en las demostraciones claras y que se pueden entender." (Tomado de "El futuro incierto de las demostraciones", de El Rincón del Vago).



Si en un triángulo ABC se construyen triángulos equiláteros exteriores sobre sus lados, los centros de dichos triángulos equiláteros determinan un triángulo equilátero (O1O2 O3) conocido como triángulo de Napoleón exterior.
Analogamente si se construyen sobre los lados del triángulo ABC triángulos equiláteros interiores, sus centros también determinan un triángulo equilátero (P1P2P3) conocido como triángulo de Napoleón interior .
Existe una interesante propiedad que relaciona las áreas de los tres triángulos: El área del triángulo ABC es igual a la diferencia de las áreas de los triángulos de Napoleón exterior e interior .
(Parece ser que Napoleón era aficionado a la Geometría y alguno de los resultados anteriores le ha sido atribuido. En cualquier caso no está muy claro que sus conocimientos geométricos fueran suficientes para llegar a establecer los resultados descritos.)
Texto Tomado de:
http://centros5.pntic.mec.es/Imagen tomada de:
www.edumat.net