Truncamiento: Aproximación de un número decimal. Para truncar un número en cierta cifra decimal se eliminan las cifras decimales que le siguen.
Ejemplo: Al truncar 23,015 a las centésimas se obtiene: 23,01
lunes, 31 de agosto de 2009
Redondeo
Redondeo: Aproximación de un número decimal. Para redondear un número en cierta cifra decimal hay que considerar el valor de la cifra siguiente: si es mayor o igual a 5, aumentas en 1 la cifra a redondear,si no, la cifra queda igual.
Ejemplo: 2,356 redondeado a dos cifras es 2,35
(Tomado de Santillana -1ro. Medio)
Ejemplo: 2,356 redondeado a dos cifras es 2,35
(Tomado de Santillana -1ro. Medio)
Teselación
Teselación : regularidad o patrón de figuras que cubre o pavimenta una superficie plana de forma que NO queden huecos y NO se traslapen las figuras.
Recta x=a, Recta Paralela al eje OY
Función Exponencial
Función Exponencial:
Es aquella cuya variable independiente es el exponente de una potencia con base positiva y distinta de 1. Su expresión:

Función Inversa
Función Inversa (tomado Santillana):
Corresponde a la expresión en la cual la variable independiente está en función de la varibale dependiente. Por ejemplo,
si y = 3x + 2, entonces x=(y-2)/3
o bien, si f(x) = 3x + 2

Cuartil, Decil
Cuartil: parte que se obtiene al dividir el total de datos en cuatro partes con igual cantidad de elementos: 25 %, 50% y 75%.
Decil: parte que se obtiene al dividir el total de datos en 10 partes con igual cantidad de elmentos: 10%, 20%, 30% ...., 90%
Decil: parte que se obtiene al dividir el total de datos en 10 partes con igual cantidad de elmentos: 10%, 20%, 30% ...., 90%
jueves, 27 de agosto de 2009
Convertir Decimal Infinito Periódico (Semiperiódico) a Fracción
Veamos la conversión de un Decimal Infinito Periódico:
Ejemplo 1:
0,2222222222 ..... a fracción
Llamamos
x = 0,2222222222 .....
10x = 2,2222222222 .....
Calculamos la diferencia: 10x - x
10x - x = 9x = 2,2222222222 ..... - 0,2222222222 .....
9x = 2
x = 2/9
Ejemplo 2:
5,2222222222 ..... a fracción
Llamamos x = 5,2222222222 .....
10x = 52,2222222222 .....
10x - x = 52,2222222222 ..... - 5,2222222222 ....
9x = 52 - 5
x= 47/9
En palabras: Para convertir una Decimal Infinito Periódico a Fracción, constrúyase una fracción:
Cuyo Numerador sea las cifras de la parte entera seguida de las cifras del periodo menos las cifras de la parte entera
Y un Denominador que tenga tantos nueves como cifras tenga el período.
5,2222222222 ..... = (52 - 5)/9
Veamos la Conversión de un Decimal Infinito Semiperiódico:
Ejemplo 1:
0,283333333333 ..... a fracción:
Llamemos x = 0,283333333333 .....
1000x = 283,3333333333 .....
100x = 28,3333333333 ....
1000x - 100x = 900x = 283-28 = 255
x= 255/900
Ejemplo 2:
1,283333333333 ..... a Fracción
Llamemos x=1,283333333333 .....
1000x=1283,333333333 .....
100x=128,3333333333 .....
1000x-100x=900x=1283-128
x=1155/900
En palabras: Para convertir un Decimal Infinito Semiperiódico a Fracción, construyase una fracción:
Cuyo numerador sea la parte entera seguida de la parte decimal no periódica y seguida del periodo menos la parte entera seguida de la parte decimal no periódica
Y un denominador que tanga tantos nueves como dígitos tenga el periodo seguidos de tantos ceros como dígitos tenga la parte decimal no periódica:
1,283333333333 ..... = (1283 - 128) / (900)
Ejemplo 1:
0,2222222222 ..... a fracción
Llamamos
x = 0,2222222222 .....
10x = 2,2222222222 .....
Calculamos la diferencia: 10x - x
10x - x = 9x = 2,2222222222 ..... - 0,2222222222 .....
9x = 2
x = 2/9
Ejemplo 2:
5,2222222222 ..... a fracción
Llamamos x = 5,2222222222 .....
10x = 52,2222222222 .....
10x - x = 52,2222222222 ..... - 5,2222222222 ....
9x = 52 - 5
x= 47/9
En palabras: Para convertir una Decimal Infinito Periódico a Fracción, constrúyase una fracción:
Cuyo Numerador sea las cifras de la parte entera seguida de las cifras del periodo menos las cifras de la parte entera
Y un Denominador que tenga tantos nueves como cifras tenga el período.
5,2222222222 ..... = (52 - 5)/9
Veamos la Conversión de un Decimal Infinito Semiperiódico:
Ejemplo 1:
0,283333333333 ..... a fracción:
Llamemos x = 0,283333333333 .....
1000x = 283,3333333333 .....
100x = 28,3333333333 ....
1000x - 100x = 900x = 283-28 = 255
x= 255/900
Ejemplo 2:
1,283333333333 ..... a Fracción
Llamemos x=1,283333333333 .....
1000x=1283,333333333 .....
100x=128,3333333333 .....
1000x-100x=900x=1283-128
x=1155/900
En palabras: Para convertir un Decimal Infinito Semiperiódico a Fracción, construyase una fracción:
Cuyo numerador sea la parte entera seguida de la parte decimal no periódica y seguida del periodo menos la parte entera seguida de la parte decimal no periódica
Y un denominador que tanga tantos nueves como dígitos tenga el periodo seguidos de tantos ceros como dígitos tenga la parte decimal no periódica:
1,283333333333 ..... = (1283 - 128) / (900)
miércoles, 26 de agosto de 2009
Desviación Media
La desviación media de un conjunto de datos es el promedio de la suma de los valores absolutos de las diferencias entre cada dato y el promedio del conjunto dado.

domingo, 23 de agosto de 2009
Cuadrado de Binomio
sábado, 22 de agosto de 2009
Porcentaje
p % signifuca tomar p partes de un total de 100 partes. Esto se expresa por medio de la fracción:
p/100
El p% de una cantidad X se expresa del modo siguiente:
p% de X implica: 

Nota: Entre Cantidades y sus porcentajes asociados
hay una relación de Directa Proporcionalidad.
Inversa Proporcionalidad
Variables Inversamente Proporcionales: Si x e y son dos variables inversamente proporcionales, entonces su relación queda representada por:

Donde k es la Constate de Proporcionalidad.
El gráfico correspondiente a esta relación es una curva llamada HIPERBOLA:

viernes, 21 de agosto de 2009
Número Intermedio
Rango de una Variable
Rango de una Variable: El rango de una variable es el conjunto de valores que puede tomar la variable. Por ejemplo: si H es la altura -medida en milímetros- del nivel de agua en un estanque de 1 metro de altura, el rango de H es el conjunto de todos los números reales entre 0 y 1000.
Número Racional
Número Racional: Todo número que se puede escribir como el cuociente de dos números enteros, con denominador no nulo.
Por ejemplo 0,45 es racional, porque se puede escribir como 45/100 = 9/20.
Pero Raíz de 2 NO es racional, porque no puede escribirse somo un cuociente de 2 números enteros. Por eso Raíz de 2 pertenece al conjunto de los Números Irracionales.
Por ejemplo 0,45 es racional, porque se puede escribir como 45/100 = 9/20.
Pero Raíz de 2 NO es racional, porque no puede escribirse somo un cuociente de 2 números enteros. Por eso Raíz de 2 pertenece al conjunto de los Números Irracionales.
Función Parte Entera
Cuerda

Cuerda: Segmento de recta que une dos puntos en una circunferencia. El diámetro es un tipo especial de cuerda.
jueves, 20 de agosto de 2009
Función Potencia
Función Potencia:
Una Función potencia está dada por la forma:

a es un número Real Distinto de Cero.
y n = 2, 3, 4, 5 ....
Un poco de análisis de la Función Potencia: Vamos a comparar en gráfica (GRAPHMATICA) el comportamiento de x al cudrado y x a la cuarta, en los intervalos [0,1] y [1, +infinito[
Principal Axioma de Probabilidad
miércoles, 19 de agosto de 2009
Rotación
ROTACION: Una rotación es una transformación que asocia a cada punto del plano una imagen de acuerdo a un punto llamado centro de rotación y a un ángulo que podemos llamar ángulo de giro.
Practicar una ROTACION:
 Se escoge un punto O llamado centro de rotación. Con el compás, se toma la medida desde el centro, hacia el vértice A y con ese radio se traza un arco de circunferencia.Marcamos el vértice rotado A’.Para rotar los otros vértices debemos medir el ángulo que corresponde al arco dibujado con el vértice A y mantenerlo, para que la forma de la figura no cambie. Además debemos conservar el ángulo de giro. La figura obtenida es congruente con la primera.
Se escoge un punto O llamado centro de rotación. Con el compás, se toma la medida desde el centro, hacia el vértice A y con ese radio se traza un arco de circunferencia.Marcamos el vértice rotado A’.Para rotar los otros vértices debemos medir el ángulo que corresponde al arco dibujado con el vértice A y mantenerlo, para que la forma de la figura no cambie. Además debemos conservar el ángulo de giro. La figura obtenida es congruente con la primera. Y ¿cómo se busca el centro de rotación? CENTRO de ROTACION: Se toma el punto medio entre A y A’ y se dibuja allí la simetral. Se toma el punto medio entre B y B’ y se dibuja allí la simetral. El punto de intersección es O.
Y ¿cómo se busca el centro de rotación? CENTRO de ROTACION: Se toma el punto medio entre A y A’ y se dibuja allí la simetral. Se toma el punto medio entre B y B’ y se dibuja allí la simetral. El punto de intersección es O. 
Rotación en sistemas de Coordendas para ángulos especiales:Rotar (4,1) con centro de rotación O= (0,0), en 90°, 180°, 270°, 360°.

Las rotaciones requeridas serán:
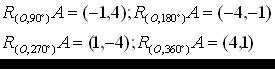 Y Resumiendo:
Y Resumiendo:
Suscribirse a:
Entradas (Atom)