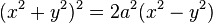Producto Punto - Forma Analítica

Producto Punto Forma Analítica

Geometría Algebraica

Geometría Algebraica:

Una de las ramas de las matemáticas que combina el álgebra abstracta con la geometría. Abarca el estudio de las formas geométricas que resultan de la representación gráfica de las soluciones de las ecuaciones algebraicas polinómicas.

Operación

Operación:

Todo conjunto formal de reglas que, aplicadas a un valor o conjuto de valores, da como resltado un nuevo valor. Las cuatro operaciones más comunes de la aritmética son la adición, la sustracción, la multiplicación y la división.

Equilibrio

Equilibrio:

En teoría de juegos, el equilibrio describe el estado de un juego en el que todos los jugadores utilizan estrategias tales que aseguran que ninguno de ellos tienen mayores posibilidades de ganar que los demás.

Mecánica Cuántica

Mecánica Cuántica:

Rama de la física en la que las fórmulas matemáticas desempeñan un papel fundamental en la descripción del movimiento y la interacción de las partículas subatómicas como, por ejemplo, en la dualidad onda partícula.

Monadología

Monadología:

La filosofía metafísica de Gottfried Leibniz tal como la expone en su obra "Monadología" (1714). Esta filosofía se basa en el concepto de las mónadas, las sustancias simples que Leibniz denominó los elementos de las cosas, cada una de las cuales está programada para comportarse de una manera determinada,

Booleana Álgebra - Álgebra Booleana - Lógica Booleana

Álgebra Booleana (Lógica Booleana):

Una de las formas del álgebra en la que las proposiciones lógicas vienen representadas mediante ecuaciones algebraicas en las que se utilizan, entre otros, los operadores "y", "o", "no", "si", y donde los números 0 y 1 representan "falso" y "verdadero" respectivamente. El álgebra booleana desempeñó (y continúa desempeñando) un papel importante en el desarrollo de programas de computación.

(50 teorías matemáticas, Brown Richard, BLUME)

Número Imaginario

Número Imaginario:

Número Figurado

Número Figurado:

Todo número que se puede representar mediante una forma geometrica regular como el triángulo, el cuadrado, o el hexágono.

Espacio de Minkowski

Espacio de Minkowski: En el año 1907 Hermann Minkowski (1864 - 1909) se dio cuenta de que la teoría especial de la relatividad podía entenderse mejor a través de una geometría no euclídea en un espacio cuatridimensional. Este espacio ha sido conocido como espacio de Minkowski. En él, el tiempo y el espacio no son entidades separadas, sino variables ligadas en un espacio de cuatro dimensiones, el espacio-tiempo. Esta representación  ayudó a Einstein en sus trabajos posteriores, que culminaron con el desarrollo de la relatividad general.

(Tomado de: "Cuando las rectas sel vuelven curvas" - Las geometrías No Euclídeas - Joan Gómez)

Ecuación Trigonométrica

Ecuación Trigonométrica: La ecuación trigonométrica es aquella cuyas incógnitas son el asunto principal de las funciones trigonométricas.

(Tomado de www.sectormatematica.cl)

Calculo Derivada Mediante Definición

Ejes Simetría - Centro de Simetría - Simetría Rotacional

Al-Khuarizmi

Muhammad ibn Musa al-Khwarizmi (813-846) es uno de los principales matemáticos árabes que en el 820 fue invitado a la corte del califa Al-Mamum para ser primero, astrónomo y más tarde jefe de la Biblioteca de la “Casa de la sabiduría” en Bagdad.

De la deformación de su nombre en las traducciones, ya que nos lo podemos enocontrar escrito como Al-Jwarizmi surge más tarde el término “algoritmo“.

Este importante matemático, conocido como el “padre del álgebra” fue por tanto bibliotecario y contribuyó además a la historia de las Enciclopedias al redactar “Mafatih al-Ulum” (o “la llave para las ciencias”) que constituye una auténtica obra enciclopédica que sintetiza las ideas científicas griegas e islámicas.

[Fuente: La historia de las Enciclopedias / Biblioteca Nacional de España ]

Destaca como matemático por:

- Su interés primordial en explicar bien las cosas y de forma clara.
- Escribir varios libros de astronomía, uno de álgebra y otro de aritmética que fueron traducidos al latín en el siglo IX.
- Sintetizar conocimientos de los griegos y de la India en distintos saberes: Matemáticas, astronomía, astrología, geografía e historia que denotan su carácter enciclopédico.

Para finalizar incluimos una cita de Mohammad Kahn que resume el buen hacer de este matemático:

“En el primer lugar del ranking de los matemáticos de todos los tiempos está al-Khwarizmi. Él escribió los trabajos más antiguos sobre aritmética y álgebra. Estos fueron la fuente principal de conocimiento matemático durante siglos tanto en oriente como en occidente. El trabajo sobre aritmética introdujo los números indios en Europa, al igual que la palabra algoritmo; y el trabajo sobre álgebra… dio su nombre a esta importante rama de las matemáticas en el mundo europeo… “. [ Fuente:http://ciencia.astroseti.org/matematicas/articulo.php?num=3819 ]

Decrecimiento Exponencial

Un ejemplo:

Número Positivo

Número Positivo: Número Mayor que Cero.

Secante a una Circunferencia

Secante a una Circunferencia: es una recta que corta a una circunferencia en dos puntos.

Radio

Radio: Segmento que une cualquier punto de una circunferencia con el centro.

Operatoria Algebraica

OPERATORIA ALGEBRAICA:

ADICIÓN DE POLINOMIOS

Para sumar y/o restar polinomios se aplican todas las reglas de reducción de términos

semejantes y uso de paréntesis.

MULTIPLICACIÓN DE POLINOMIOS

MONOMIO POR MONOMIO:

Se multiplican los coeficientes numéricos entre sí y los factores literales entre sí usando propiedades de potencias. En el caso de multiplicar un monomio por un producto de

monomios se multiplica sólo por uno de ellos. Es decir,

a · (b · c) = (a · b) · c

MONOMIO POR POLINOMIO:

Se multiplica el monomio por cada término del polinomio.

Es decir, a(b + c + d) = ab + ac + ad

POLINOMIO POR POLINOMIO:

Se multiplica cada término del primer polinomio por cada término del segundo polinomio

y se reducen los términos semejantes, si los hay.

(Recopilación de A. Sánchez)

Fracción Decimal

Fracción Decimal: Fracción que tene como denominador una (cualquiera) potencia de 10.

Escala

Escala: Razón de semejanza en un mapa o dibujo que es copia reducida o aumentada del original.

Rectas Convergentes

Rectas Convergentes: Rectas que tienen un punto en común.

Homogéneo

Homogéneo: Formado por elementos de una misma naturaleza.

Reflexión de Punto respecto de Ejes Cartesianos

Número Sordo

Número Sordo: Número que NO tiene raíz exacta.

Operación Binaria

Operación Binaria: Operación que se realiza con dos elementos al mismo tiempo.

Geometría Plana

Geometría Plana: Trata de figuras cuyos puntos o líneas se encuentran todos contenidos en un plano.

Levógiro y Dextrógiro

Levógiro y Dextrógiro:

3 Representaciones Sistema de Ecuaciones

Sucesión Monótona Decreciente

Sucesión Monótona Decreciente: Sucesión en la cual un término cualquiera es mayor o igual que el siguiente.

Regla de Barrow

(Tomado de Wikipedia)

Geometría del Espacio

Geometría del Espacio: Trata de figuras cuyos elementos no todos están en un mismo plano.

Círculo Unitario

Círculo Unitario: Ver en este mismo blog: "Círculo Goniométrico".

Semi

Semi: Prefijo que consigna MITAD.

Residuo / Resto

Residuo, Resto: La cantidad que sobra luego de una división (como pasa si un número no puede ser dividido exactamente por otro).

Ejemplo: 19 no puede ser dividido exactamente por 5. Lo más cerca que se puede llegar sin pasarse es 3 x 5 = 15, lo cual es 4 menos que 19.

Entonces la Respuesta de 19 ÷ 5 es 3 con un residuo de 4.

(Tomado de Disfruta las Matemáticas)

Lateral

Lateral: Relativo a los bordes de los polígonos o a las caras de los poliedros.

Polinomio

Polinomio: En matemáticas, se denomina polinomio a la suma de varios monomios (llamados términos del polinomio).

Rectas Convergentes

Rectas Convergentes: Rectas que tienen un punto en común.

Radical

Radical: Simbolo que indica la operación de extraer raíz.

Kilo

Kilo: Prefijo que significa mil.

Polinomio

Polinomio: Expresión algebraica formada por la suma (o resta) de varios monomios.

Dimensión de un Espacio

Dimensión de un espacio: es el número de coordenadas independientes necesarias para especificar las cosas que pertenecen a él.

Vectores Unitarios (Video Tomado de Las Matemáticas)

Potenciación - Radicación - Logaritmación: Tres Operaciones Nexadas

Función como Máquina

Posición Relativa de 2 Rectas en el Plano

Posición Relativa de 2 Rectas en el Plano:

Hacer Click en la imagen para agrandar

Sumatorias Conocidas

Sumatorias Conocidas:

(Tomado de Revista Ábaco - UACH)

Antilogaritmo

Desigualdad Triangular y Complejos

Hacer click para agrandar

Hipocicloide

CURVAS CÍCLICAS

Una hipocicloide como la de la imagen es una curva generada por un punto sobre una circunferencia que rueda sin deslizamiento dentro de otra circunferencia mayor. Dependiento de la relación de los radios, se forman distintas figuras. En la foto, el radio de la circunferencia interior es un tercio del radio de la circunferencia exterior.

Las hipocicloides pertenecen a la familia de las curvas hipotrocoides. Las hipotrocoides son las curvas generadas por un punto fijo respecto de una circunferencia que rueda sin deslizamiento por el interior de otra circunferencia. Las hipocicloides son hipotrocoides en las que el punto fijo está sobre la propia circunferencia interior (su distancia al centro de esta circunferencia es r, el radio de ésta).

A su vez, las hipotrocoides pertenecen a la familia más general de las curvas cíclicas, de las que forman parte también las epitrocoides y las trocoides.

En las epitrocoides, la curva es generada por el movimiento de un punto fijo respecto de una circunferencia que rueda sin deslizamiento por exterior de otra circunferencia. A esta familia pertenecen los epiciclos, los Caracoles de Pascal y los cardioides.

En los trocoides, la curva es generada por un punto fijo respecto de una circunferencia que rueda sobre una recta. La cicloide pertenece a esta familia.

   

Esponja de Menger

LA ESPONJA DE MENGER

Cómo construir la esponja de Menger:

1) Se toma un cubo
2) Se divide en 27 cubos iguales, dividiendo cada arista en tres, como si fuera un cubo de Rubik.
3) Se elimina el subcubo central de cada cara y el subcubo central del cubo.
4) Para cada uno de los 20 subcubos restantes se aplica el procedimiento anterior.

y luego se sigue, teóricamente, a infinito .... este proceso!

La esponja de Menger es un fractal de dimensión aproximada 2,7268.

 

Infinito (Signo del)

En tiempos modernos, para describir una cantidad cuyo valor numérico es imposible ser escrito, utilizamos el símbolo ∞. Fue reintroducido por el profesor de Oxford John Wallis en 1655 para denominar una cantidad infinita. ¿Reintroducido? Si, debido a que los romanos lo utilizaban para representar el número 1000. Al pasar del tiempo, le alteraron su significado para denotar cualquier cantidad grande de elementos.Ya de ahí, el resto es historia. 

Hipótesis de Riemann

Hipótesis de Riemann:

Función Zeta de Riemann

Función Zeta de Riemann:

Aritméticas Operaciones

Operaciones Aritméticas:

Teorema del Valor Intermedio

Teorema del Valor Intermedio: 


Si f es una función continua en el itervalo cerrado{a,b} y se tiene que c es un número entre f(a) y f(b), entonces existe un Xo en el intervalo {a,b} tal que f(Xo)=c.

Graficamente esto es muy fácil de visualizar:

Cubo - Diagonales de cara y cubo

Propiedades de la PARIDAD

Propiedades de la PARIDAD:


1) La suma de dos números pares es un número par:
(2n) + (2n+2) = 4n +2 = 2(2n +2) : es par.


2) La suma de dos números impares es un número par:
(2n+1) + (2n+3) = 4n + 4 = 2(2n+2) : es par.


3) La suma de un número par más otro impar es un número impar.
(2n+1) + (2n) = 4n + 1 = 2(2n) + 1 : es impar.


4) El producto de dos números pares es par:
(2n)(2k) = 4 nk = 2(2nk) : es par.


5) El producto de dos números impares es imapr:
(2n+1)(2k-1) = 2nk - 2n + 2k -1 = 2(nk-n+k) - 1: es impar.


6) El producto de un número impar por otro par es par:
(2n)(2k+1) = 4nk + 2n = 2(2nk+n) : es par.


7) El cuadrado de un número par es par:
(2n)(2n) = 4(n)(n) = 2 (2nn) : es par.


8) El cuadrado de un número impar es impar:
(2n+1)(2n+1) = 4nn + 2n + 2n + 1 = 2(2nn + 2n) + 1 : es impar. 

Demostración - Ejemplo

Tesis:

Hipóstesis:

Demostración:

División Interior Trazo - Método Gráfico

Por ejemplo, dividamos un trazo en la razón de 7 : 3

Teorema de los Números Primos (de Wikipedia)

Varianza y Desviación Estándar de Variable Aleatoria Discreta

Conversión entre Forma Polar y Forma Binomial de un Complejo

Conversión entre Forma Polar y Forma Binomial de un Complejo:

y de forma más completa:


COORDENADAS POLARES DE UN COMPLEJO:

Solución Ecuación de Cuarto Grado

Solución Ecuación de Cuarto Grado:

Poliedro de Császar (Tomado de Gaussianos)

¿Qué es el poliedro de Császár?

El poliedro de Császár es un poliedro no convexo que no tiene diagonales (comparte esta propiedad con el tetraedro), es decir, cada uno de sus vértices está conectado con todos los demás por una arista. Podemos verlo en la siguiente imagen (tomada deMathWorld):

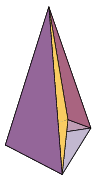
En este enlace de la Wikipedia podéis ver una animación de este poliedro junto con la figura que queda al desplegarlo.

El poliedro de Császár tiene 7 vértices, 21 aristas y 14 caras triangulares. Por ello no cumple la fórmula de Euler:

Es topológicamente equivalente a un toro (esto es, una rosquilla) y su esqueleto es isomorfo al grafo completo .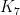

Este poliedro fue descubierto por el topólogo húngaro Ákos Császár en 1949 y sirvió para resolver el siguiente problema:

Un toroide es un poliedro cuyas caras son todas polígonos simples (es decir, si fueran de plastilina podríamos deformarlas sin romperlas hasta obtener un disco) que además cumple que el propio poliedro es topológicamente equivalente a una esfera con uno o más agujeros que la atraviesan. ¿Es posible construir un toroide que no posea diagonales?

¿Cómo construir el poliedro de császár?

A la vista de la imagen anterior, el poliedro de Császár tiene una forma muy peculiar, extraña, hasta difícil de imaginar. Lo curioso es que es sencillo construirlo con papel a partir de estas dos plantillas:

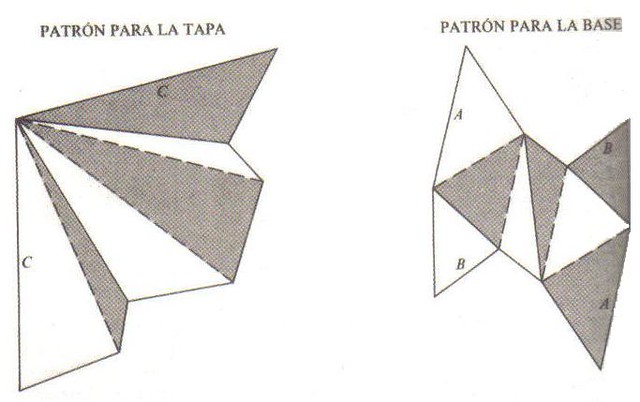
Los pasos que debemos seguir para contruir el poliedro, según el gran Martin Gardner, con los siguientes:

Recortamos las plantillas y coloreamos por los dos lados los triángulos sombreados. Después doblamos por las líneas de puntos para formar aristas “montañas” y por las líneas llenas para formar aristas “valle”.

Para formar la base plegamos los dos triángulos más grandes hacia el centro y sujetamos con cinta adhesiva los vértices A uno junto al otro. Le damos la vuelta al papel y plegamos los triángulos más pequeños hacia el centro sujetando después con cinta las aristas B. Ya tenemos la base.

La punta cónica de seis caras se forma pegando entre sí los lados C. Para colocarla sobre la base se unen los triángulos blancos con los triángulos sombreados y después se pegan cada uno de sus seis lados a los seis correspondientes de la base.

Hemos comentado antes que este poliedro no tiene diagonales y que el poliedro de Császár y el tetraedro son los únicos poliedros conocidos (con superficie acotada) que no tienen diagonales. Es sencillo comprobar que si un poliedro tiene  vértices y agujeros, el hecho de que no posea diagonales obliga a que se cumpla la siguiente relación:

Teniendo en cuenta que los dos tienes que ser números enteros positivos y que además debe ser mayor que 3 (no hay poliedro con 3 o menos vértices), la solución con valores más pequeños es 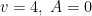, que corresponde al tetraedro. Y la siguiente es 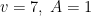, que es la que corresponde al poliedro de Császar. La siguiente solución posible es , que nos daría un poliedro con 44 caras y 66 lados, pero dicho poliedro no puede construirse. No se conoce ninguna solución más a partir de la cual se obtenga un poliedro que se pueda construir.

Por Defecto

Aproximación Por Defecto: Es una aproximación que es menor que el valor real.

Serie Alternada

Serie Alternada: Serie de números reales cuyo término general provoca términos particulares que alternan entre positivo y negativo.

Cono de Apolonio - Imagen

Cono de Apolonio:

GPS

GPS: (Sistema de Posicionamiento Global), permite determinar con alta precisión la posición tridimensional (altitud, Longitud y altitud) de un punto en nuestro planeta.

El GPS funciona con 24 satçelites distribuidos en 6 órbitas con un período de 12 horas, con una amplitud aproximada de 20.200 Km y una inclinación de 55º respecto del plano ecuatorial.

Novedad del Colectivo Bourbaki (Un sueño Euclideano)

El punto de partida del colectivo Bourbaki fue la teoría de conjuntos. La idea era derivar TODO el universo matemático desde un único punto inicial: la teoría de Conjuntos, como anteriormente, en la antiguedad, Euclides había derivado todo el andamiaje geométrico de nociones básicas o primitivas.

El propósito del colectivo era poner en relieve la unidad de las matemáticas. El propósito era escribir libros, definir elementos matemáticos siguiendo  métodos axiomáticos que nunca se apartasen del objetivo de la formalización absoluta. El tratado de las matemáticas debía ser lo más riguroso posible.

Para lo anterior utilizó dos métodos muy eficaces: Uno era la axiomatización y el otro la inclusión de la noción general de estructura. La axiomatización fue tomada directamente de Euclides -mejorada más tarde por Hilbert- y la noción de estructura en gran parte creada por el colectivo Bourbaki y en parte tomada de los avances linguísticos de la época.


En el futuro, la decisión de arrancar el edificio axiomático Bourbakiano desde la Teoría de Conjuntos, preñada de profundas paradojas e incoherencias, repercutió en la continuidad del sueño del colectivo Bourbaki.

Bourbaki Nicolás

Bourbaki Nicolás: Grupo de matemáticos franceses que para los entornos de 1930 provocó una completa revolución en las matemáticas del orbe entero, cuestión que incluso repercutió en muchas otras ciencias, incluso en las ciencias sociales. El nombre de Nicolás Bourbaki, que asociaron al matemático autor de muchas publicaciones, no corresponde a un matemático de existencia real, proviene de bromas estudiantiles hechas en la escuela normal de Francia, en la que los estudiantes asustaban a los novatos con Teoremas inexistentes de un tal Bourbaki, que en la historia real correspondió a un militar de relativa fama.

El colectivo Boubaki fundó su creación en el punto de partida elemental: la teoría de conjuntos desde donde derivaron un universo matemático de gran amplitud en donde las perspectivas de rigurosidad axiomática y la estructura matemática fueron muy relevantes.

El grupo Bourbaki revolucionó el quehacer matemático en la Francia de la posguerra.

de Wikipedia:

Nicolas Bourbaki es el nombre colectivo de un grupo de matemáticos franceses que en los años 30 del siglo XX se propusieron revisar los fundamentos de las matemáticas con una exigencia de rigor mucho mayor que la que entonces era moneda corriente en esta ciencia. Fundado en 1935, inició la publicación de sus monumentales Elementos de matemáticas de acuerdo con el nuevo canon de rigor y el método axiomático, pretendiendo cubrir las bases de todas las matemáticas. Hasta el presente (2006) ha redactado los volúmenes de «Teoría de conjuntos», «Álgebra», «Topología general», «Funciones de una variable real», «Espacios vectoriales topológicos», «Integración», «Álgebra conmutativa», «Variedades diferenciables y analíticas», «Grupos yálgebras de Lie» y «Teorías espectrales». Estos volúmenes contienen notas históricas que han sido publicadas aparte, formando unos apreciados, aunque muy incompletos aún (2006) volúmenes cuyo corpus recibe el nombre de Elementos de Historia de las Matemáticas.

Su impacto en las matemáticas contemporáneas ha sido enorme, y desde los años 50 puede decirse que su exigencia de rigor ha sido universalmente aceptada en matemáticas, junto con el estilo particular en que la expresan, siendo muy diferentes los textos actuales de los prebourbakianos. Este éxito ha vuelto innecesaria la continuación de su obra, pues desde los años 60todos los textos se redactan ya siguiendo sus exigencias. No obstante, en París sigue desarrollándose el Seminario Bourbaki, donde cada año se exponen los principales avances de las matemáticas.

La "tragedia" de este titánico intento de fundamentar todas las matemáticas es que eligieron como punto de partida la teoría de conjuntos y, cuando en los años 1950 y 1960 apareció la teoría de categorías como supuesto principio unificador de todas las matemáticas conocidas, decidieron con pleno conocimiento de causa no seguir ese camino («ese infierno» en sus propias palabras) renunciando así a su propósito inicial.

Desde el principio trataron de mantener la simpática ficción de que Nicolas Bourbaki era un matemático «poldavo». Por eso el nombre de sus miembros, que cambian a lo largo del tiempo, es uno de los secretos mejor guardados (al igual que su forma de organizarse), aunque se sabe que en su mayoría son franceses. En su página web ya reconocen que fue fundado inicialmente por Henri Cartan, Claude Chevalley, Jean Coulomb, Jean Delsarte, Jean Dieudonné, Charles Ehresmann, René de Possel, Szolem Mandelbrojt y André Weil. Eran antiguos alumnos de la Escuela Normal Superior de París que, a iniciativa de Cartan y Weil y bajo el grito de guerra "todos deben interesarse en todo", se propusieron redactar textos nuevos para sus clases. Parece seguro que los mejores matemáticos franceses de mediados del siglo XX (Jean-Pierre Serre, Alexandre Grothendieck, Laurent Schwartz,Pierre Samuel, Jean-Louis Koszul, Armand Borel, Pierre Cartier, Roger Godement, ...) en algún momento han formado parte, al igual que alguno de otra nacionalidad (Samuel Eilenberg, John Tate, ...).

Página Oficial del Grupo Bourbaki: Grupo Bourbaki - Página Oficial

Lemniscata

Lemniscata:

de wikipedia: 

En matemática, una lemniscata es un tipo de curva descrita por la siguienteecuación en coordenadas cartesianas:

La representación gráfica de esta ecuación genera una curva similar a . La curva se ha convertido en el símbolo del infinito y es ampliamente utilizada en matemática. El símbolo en sí mismo es, a veces, llamado lemniscata. Su representación en Unicode es ∞ y su código es (∞).

La lemniscata fue descrita por primera vez en 1694 por Jakob Bernoulli como la modificación de una elipse, curva que se define como el lugar geométrico de los puntos tales que la suma de las distancias desde dos puntos focales es unaconstante. En contraposición, una lemniscata es el lugar geométrico de los puntos tales que el producto de estas distancias es constante. Bernoulli la llamólemniscus, que en Latín significa "cinta colgante".

La lemniscata puede ser obtenida como la transformada inversa de una hipérbola, con el círculo inversor centrado en el centro de la hipérbola (punto medio del segmento que une los dos focos).