Poliedro de Császar (Tomado de Gaussianos)

¿Qué es el poliedro de Császár?

El poliedro de Császár es un poliedro no convexo que no tiene diagonales (comparte esta propiedad con el tetraedro), es decir, cada uno de sus vértices está conectado con todos los demás por una arista. Podemos verlo en la siguiente imagen (tomada deMathWorld):

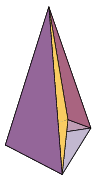
En este enlace de la Wikipedia podéis ver una animación de este poliedro junto con la figura que queda al desplegarlo.

El poliedro de Császár tiene 7 vértices, 21 aristas y 14 caras triangulares. Por ello no cumple la fórmula de Euler:

Es topológicamente equivalente a un toro (esto es, una rosquilla) y su esqueleto es isomorfo al grafo completo .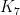

Este poliedro fue descubierto por el topólogo húngaro Ákos Császár en 1949 y sirvió para resolver el siguiente problema:

Un toroide es un poliedro cuyas caras son todas polígonos simples (es decir, si fueran de plastilina podríamos deformarlas sin romperlas hasta obtener un disco) que además cumple que el propio poliedro es topológicamente equivalente a una esfera con uno o más agujeros que la atraviesan. ¿Es posible construir un toroide que no posea diagonales?

¿Cómo construir el poliedro de császár?

A la vista de la imagen anterior, el poliedro de Császár tiene una forma muy peculiar, extraña, hasta difícil de imaginar. Lo curioso es que es sencillo construirlo con papel a partir de estas dos plantillas:

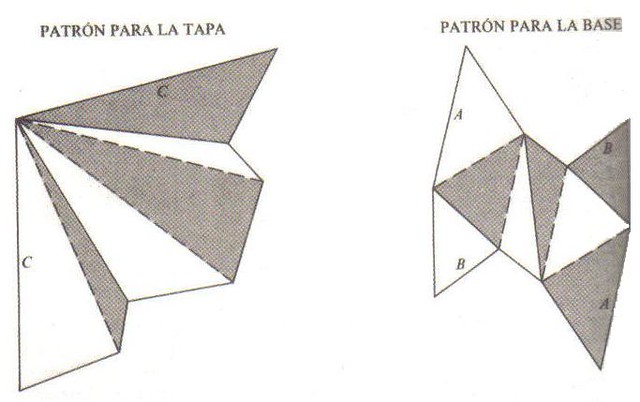
Los pasos que debemos seguir para contruir el poliedro, según el gran Martin Gardner, con los siguientes:

Recortamos las plantillas y coloreamos por los dos lados los triángulos sombreados. Después doblamos por las líneas de puntos para formar aristas “montañas” y por las líneas llenas para formar aristas “valle”.

Para formar la base plegamos los dos triángulos más grandes hacia el centro y sujetamos con cinta adhesiva los vértices A uno junto al otro. Le damos la vuelta al papel y plegamos los triángulos más pequeños hacia el centro sujetando después con cinta las aristas B. Ya tenemos la base.

La punta cónica de seis caras se forma pegando entre sí los lados C. Para colocarla sobre la base se unen los triángulos blancos con los triángulos sombreados y después se pegan cada uno de sus seis lados a los seis correspondientes de la base.

Hemos comentado antes que este poliedro no tiene diagonales y que el poliedro de Császár y el tetraedro son los únicos poliedros conocidos (con superficie acotada) que no tienen diagonales. Es sencillo comprobar que si un poliedro tiene  vértices y agujeros, el hecho de que no posea diagonales obliga a que se cumpla la siguiente relación:

Teniendo en cuenta que los dos tienes que ser números enteros positivos y que además debe ser mayor que 3 (no hay poliedro con 3 o menos vértices), la solución con valores más pequeños es 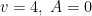, que corresponde al tetraedro. Y la siguiente es 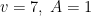, que es la que corresponde al poliedro de Császar. La siguiente solución posible es , que nos daría un poliedro con 44 caras y 66 lados, pero dicho poliedro no puede construirse. No se conoce ninguna solución más a partir de la cual se obtenga un poliedro que se pueda construir.