Números de Liouville

Ya en 1844, Joseph Liouville estudió este número:

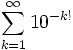	= 0.11000100000000000000000100……
	(cada cifra es 1 si está n! posiciones después del punto decimal, y 0 si no.)

Es un número muy interesante porque:

• es irracional, y
• además no es solución de ninguna ecuación polinomial así que no es algebraico.

De hecho, Joseph Liouville acababa de encontrar el primer número transcendente que se podía demostrar que lo era.

Ese número se conoce ahora como la constante de Liouville. Y es un número de Liouville.

Un número de Liouville es un tipo especial de número transcendente que se puede aproximar muy de cerca con números racionales.

Más formalmente es un número real x, con la propiedad de que, para cada entero positivo n, existen dos enteros p y q (con q>1) que cumplen:

(Tomado de Disfruta las Matemáticas)