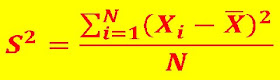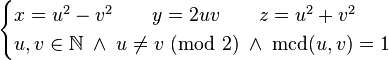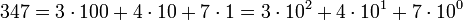Los ángulos opuestos de un cuadrilátero inscrito en una circunferencia son SUPLEMENTARIOS.
miércoles, 28 de octubre de 2009
Ecuación Diofántica
(Tomado de Wikipedia)
o los números naturales 
, es decir, se trata de ecuaciones cuyas soluciones son números enteros.Un ejemplo de ecuación diofántica es: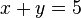 
Esta ecuación tiene infinitas soluciones en los números reales. Como regla general, sin embargo, las ecuaciones que aparecen en los problemas tienen restricciones que nos ayudan a limitarnos a un pequeño número de casos e incluso a una única solución.
Por ejemplo, en nuestra ecuación, si restringimos los posibles valores de x e y a los enteros positivos, tenemos 4 soluciones para (x,y):
- (1,4) (2,3) (3,2) (4,1).
Un problema matemático muy famoso que se resuelve por medio de ecuaciones diofánticas es el del mono y los cocos.
Un caso Particular de Ecuación Diofántica: Ecuación pitagórica
Se llama ecuación pitagórica a la ecuaci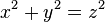ón 
con 
. Cualquier terna (x, y, z) solución de la ecuación anterior se conoce como terna pitagórica. Además si (x, y, z) es una terna pitagórica solución de la ecuación pitagórica también lo serán:
- La terna alternando x e y: (y, x, z).
- Una terna múltiplo (ky, kx, kz).
- Una terna con algún signo cambiado (-x, y, z), (x, -y, z) o (y, x, -z)
- Cualquier otra terna obtenida mediante una combinación de los procedimientos anteriores.
Se dice que una terna es primitiva, si el máximo común divisor de x, y, z es la unidad, es decir, mcd(x,y,z) = 1. En toda terna primitiva al menos uno de los números x o y es par y z es impar. Puede verse que en esas condiciones todas las ternas primitivas que son de la ecuación pitagórica son de la forma:
martes, 27 de octubre de 2009
miércoles, 21 de octubre de 2009
Método de Completación de Cuadrados (pro resolver ecuaciones de segundo grado)
Método de Completación de Cuadrados - Pro resolver Ecuación de Segundo Grado: Consiste en expresar el polinomio de segundo grado:
como la suma de un cuadrado de binomio y de una constante.
Veamos un ejemplo MUY concreto:
Proyección de Cateto sobre Hipotenusa
Proyección de Cateto sobre Hipotenusa: Segmento contenido en la hipotenusa que une el pie de la altura trazada desde el vértice del ángulo recto con uno de los otros vértices.
Estas proyecciones son importantes en el teorema de Euclides.
sábado, 17 de octubre de 2009
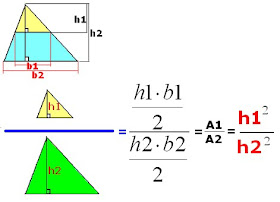
Razón de las Áreas de 2 Triángulos Semejantes
Partamos de un Teorema un poquito más GENERAL:
"Las áreas de los triángulos semejantes son entre sí
como los cuadrados de dos lados homólogos."
Y en particular, lo que anunciábamos:
Razón entre las Áreas de 2 Triángulos Semejantes:
LA RAZÓN ENTRE LAS ÁREAS DE DOS TRIÁNGULOS SEMEJANTES ES COMO LA RAZÓN ENTRE LOS CUADRADOS DE LAS ALTURAS CORRESPONDIENTES ...
martes, 13 de octubre de 2009
Términos Semejantes
En el siguiente ejemplo son semejantes el primero, el segundo y el tercero de los términos (aunque éste último tenga el factor literal con las letras en otro orden) .... el cuarto no es semejante a los anteriores porque incluye la "ñ" ....
Número Impar
Número Impar: Un número es impar si y sólo si NO es par.
n es impar si y sólo si n = 2p - 1, con p perteneciente a N (Naturales)
Número Par
Número Par: Un número natural es par si y sólo sí es múltiplo de 2.
n es par si y sólo si n = 2p, con p perteneciente a N (Naturales)
Máximo Común Divisor - m.c.d.
El Máximo Común Divisor (m.c.d.): de un conjunto de números naturales es el mayor número natural que divide a cada uno de los números dados.
Para determinar el m.c.d. hay varios métodos, uno de ellos es descomponer cada uno de los números del -conjunto de números- en sus factores primos. Luego se eligen los factores primos presentes de forma común en cada uno de los números con sus menores exponentes ....
Ejemplo: Buscar el m.c.d. entre 60 y 280
60 = 2x2x3x5
140=2x2x2x5x7
El m.c.d. es: 2x2x5=20
2 elevado a 2 por 5 elevado a 1=20. El 2 y el 5 están presentes en ambos, elegimos 2 elevado a 2 pese a que en uno de los números está presente al cubo.
Teorema Fundamental Aritmética
Teorema Fundamental de la Aritmética: Todo número compuesto se puede descomponer de manera única como producto de dos primos.
Este teorema sirve para interrelacionar los números primos y los compuestos.
Ejemplo: 105 es compuesto, se puede poner como el producto de tres factores: 3 x 5 x 7 = 105
3, 5 y 7 son números primos ....
Número Cpmpuesto
Número Compuesto: Un número natural n mayor que 1 es compuesto sí y sólo sí ese número NO es primo.
Ejemplo: 6 es compuesto puesto que no es primo: 6 = 2 x 3
Nota: El número 1 no es ni primo ni compuesto.
viernes, 9 de octubre de 2009
Sistema (de Numeración) Decimal
El sistema decimal es un sistema de numeración en el que las cantidades se representan utilizando como base el número diez, por lo que se compone de diez cifras diferentes:
cero (0); uno (1); dos (2); tres (3); cuatro (4); cinco (5); seis (6); siete (7); ocho (8) y nueve (9).
Este conjunto de símbolos se denomina números árabes, y es de origen indio.
Es el sistema de numeración usado habitualmente en todo el mundo (excepto ciertas culturas) y en todas las áreas que requieren de un sistema de numeración. Sin embargo hay ciertas técnicas, como por ejemplo en la informática, donde se utilizan sistemas de numeración adaptados al método de trabajo como el binario o el hexadecimal. También pueden existir en algunos idiomas vestigios del uso de otros sistemas de numeración, como el quinario, el duodecimal y el vigesimal. Por ejemplo, cuando se cuentan artículos por docenas, o cuando se emplean palabras especiales para designar ciertos números (en francés, por ejemplo, el número 80 se expresa como "cuatro veintenas").
Según los antropólogos, el origen del sistema decimal está en los diez dedos que tenemos los humanos en las manos, los cuales siempre nos han servido de base para contar.
El sistema decimal es un sistema de numeración posicional, por lo que el valor del dígito depende de su posición dentro del número. Así:
Los números decimales se pueden representar en rectas numéricas.
(Tomado de Wikipedia)
jueves, 8 de octubre de 2009
Función Afín
Función Afín: Una función Afín es aquella que esta determinada por una ecuacion de primer grado de la forma:
y = f(x) = mx + n con m y n constantes
La ecuacion de una funcion afn es conocida como ecuacion de la recta, debido a que
las gráficas de todas las funciones de esta forma son precisamente lineas rectas.
Números Reales
Números Reales: Es el conjunto que obtenemos entre la union de los conjuntos Racionales e Irracionales:
Los números Racionales tienen representación decimal periódica y los irracionales representación decimal no periódica.
Conjuntos Numéricos
R: Números Reales
Q: Números racionales
I: Números Irracionales ( Q* )
Z: Números Enteros.
N: Números Naturales
(En algunos textos se uasn los "No: Números Cardinales" que la unión de los Naturales y el cero)
miércoles, 7 de octubre de 2009
Ángulo Elevacion - Ángulo Depresión
Ángulos de elevación y de Depresión: Son aquellos formados por la horizontal, considerada a nivel del ojo del observador y la linea de mira, segun que el objeto observado este por sobre o bajo esta ultima.
Fuente: Resumen PSU Matemática - Álvaro Sánchez Vásquez
Prioridad de Operaciones
PRIORIDAD DE LAS OPERACIONES
Al realizar distintas operaciones a la vez, se debe respetar el siguiente orden:
1. Resolver los parentesis.
2. Realizar las potencias.
3. Realizar multiplicaciones y/o divisiones de izquierda a derecha.
4. Realizar adiciones y/o sustracciones de izquierda a derecha.
Al realizar distintas operaciones a la vez, se debe respetar el siguiente orden:
1. Resolver los parentesis.
2. Realizar las potencias.
3. Realizar multiplicaciones y/o divisiones de izquierda a derecha.
4. Realizar adiciones y/o sustracciones de izquierda a derecha.
Números Naturales - Números Cardinales
NÚMEROS NATURALES Y NUMEROS CARDINALES ( cuyos símbolos son: IN, IN0 )
Los elementos del conjunto
se denominan “Números Naturales”. El término Natural quizás provenga del hecho de ser los números que naturalmente se usan para contar.
Si a este conjunto le unimos el conjunto formado por el cero, obtenemos
llamado “conjunto de los números cardinales”.
Los elementos del conjunto
lN = {1, 2, 3, …}
se denominan “Números Naturales”. El término Natural quizás provenga del hecho de ser los números que naturalmente se usan para contar.
Si a este conjunto le unimos el conjunto formado por el cero, obtenemos
lN0 = {0, 1, 2, …}
llamado “conjunto de los números cardinales”.
Reglas de Divisibilidad
Un número es divisible por:
2 Si Termina en cifra par.
3 Si La suma de sus cifras es multiplo de tres.
4 Si Las dos ultimas cifras forman un numero multiplo de cuatro o bien
son Ceros.
5 Si La ultima cifra es cero o cinco.
6 Si Es divisible por dos y por tres a la vez.
7 Si La diferencia entre el doble de la ultima cifra y el numero que forman las Cifras restantes es multiplo de siete.
8 Si Las tres ultimas cifras forman un numero multiplo de ocho o bien son Ceros.
9 Si La suma de sus cifras es multiplo de nueve.
10 Si Termina en cero.
11 Si La diferencia entre la suma de las cifras ubicadas en los lugares pares y las que ocupan los lugares impares es multiplo de once.
2 Si Termina en cifra par.
3 Si La suma de sus cifras es multiplo de tres.
4 Si Las dos ultimas cifras forman un numero multiplo de cuatro o bien
son Ceros.
5 Si La ultima cifra es cero o cinco.
6 Si Es divisible por dos y por tres a la vez.
7 Si La diferencia entre el doble de la ultima cifra y el numero que forman las Cifras restantes es multiplo de siete.
8 Si Las tres ultimas cifras forman un numero multiplo de ocho o bien son Ceros.
9 Si La suma de sus cifras es multiplo de nueve.
10 Si Termina en cero.
11 Si La diferencia entre la suma de las cifras ubicadas en los lugares pares y las que ocupan los lugares impares es multiplo de once.
martes, 6 de octubre de 2009
lunes, 5 de octubre de 2009
viernes, 2 de octubre de 2009
Estadística
Estadísticas: Ciencia que estudia los fenómenos o experimentos aleatorios, ocupándose de recoger y ordenar un gran número de datos, con el fin de obtener alguna consecuencia.
La rama de la estadística que se ocupa de representar los datos, recibe el nombre de Estadística Descriptiva.
La parte de la estadística que trata de extraer conclusiones recibe el nombre de Estadística Inductiva o Inferencial.
jueves, 1 de octubre de 2009
Media Aritmética o Promedio
Media Aritmética o Promedio: Se define como el cuociente entre la suma de los valores de la variable (datos) y el total de datos.
Varianza
Varianza: Es la medida aritmética de los cuadrados de las desviaciones. Se denota por y su fórmula es:
N es el número TOTAL de datos.
Este valor cuantifica el grado de dispersión o separación de los valores de la distribución con respecto a la media aritmética. A mayor dispersión mayor valor de la varianza, a menor dispersión menor valor de la varianza.
Rango
Rango: Es la primera medida de dispersión. Se define como la diferencia entre el mayor y el menor de los datos de la distribución. No es medida significativa, pues sólo indica cuan dispersos están los datos entre los extremos.
R = (X máx) - (X min)