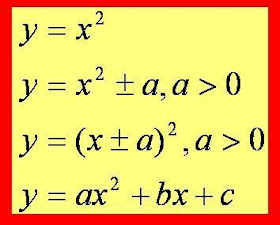Truncamiento

Truncamiento: Aproximación de un número decimal. Para truncar un número en cierta cifra decimal se eliminan las cifras decimales que le siguen.

Ejemplo: Al truncar 23,015 a las centésimas se obtiene: 23,01

Redondeo

Redondeo: Aproximación de un número decimal. Para redondear un número en cierta cifra decimal hay que considerar el valor de la cifra siguiente: si es mayor o igual a 5, aumentas en 1 la cifra a redondear,si no, la cifra queda igual.

Ejemplo: 2,356 redondeado a dos cifras es 2,35

(Tomado de Santillana -1ro. Medio)

Teselación

Teselación : regularidad o patrón de figuras que cubre o pavimenta una superficie plana de forma que NO queden huecos y NO se traslapen las figuras.

Volumen Pirámide

Recta x=a, Recta Paralela al eje OY

Es una recta que es paralela al eje OY, que siempre mantiene para con este eje la distancia "a", independiente del valor de Y.

Volumen y Area en un Cono (Area Lateral, Basal y Total)

Función Exponencial

Función Exponencial:

Es aquella cuya variable independiente es el exponente de una potencia con base positiva y distinta de 1. Su expresión:

Función Inversa

Función Inversa (tomado Santillana):

Corresponde a la expresión en la cual la variable independiente está en función de la varibale dependiente. Por ejemplo,

si y = 3x + 2, entonces x=(y-2)/3

o bien, si f(x) = 3x + 2

Cuartil, Decil

Cuartil: parte que se obtiene al dividir el total de datos en cuatro partes con igual cantidad de elementos: 25 %, 50% y 75%.

Decil: parte que se obtiene al dividir el total de datos en 10 partes con igual cantidad de elmentos: 10%, 20%, 30% ...., 90%

Teorema de Euler

En todo cuerpo poliedro convexo se verifica la siguiente relación:

Convertir Decimal Infinito Periódico (Semiperiódico) a Fracción

Veamos la conversión de un Decimal Infinito Periódico:

Ejemplo 1:

0,2222222222 ..... a fracción
Llamamos
x = 0,2222222222 .....
10x = 2,2222222222 .....
Calculamos la diferencia: 10x - x
10x - x = 9x = 2,2222222222 ..... - 0,2222222222 .....
9x = 2
x = 2/9

Ejemplo 2:

5,2222222222 ..... a fracción
Llamamos x = 5,2222222222 .....
10x = 52,2222222222 .....
10x - x = 52,2222222222 ..... - 5,2222222222 ....
9x = 52 - 5
x= 47/9

En palabras: Para convertir una Decimal Infinito Periódico a Fracción, constrúyase una fracción:

Cuyo Numerador sea las cifras de la parte entera seguida de las cifras del periodo menos las cifras de la parte entera

Y un Denominador que tenga tantos nueves como cifras tenga el período.

5,2222222222 ..... = (52 - 5)/9

Veamos la Conversión de un Decimal Infinito Semiperiódico:

Ejemplo 1:
0,283333333333 ..... a fracción:
Llamemos x = 0,283333333333 .....
1000x = 283,3333333333 .....
100x = 28,3333333333 ....
1000x - 100x = 900x = 283-28 = 255
x= 255/900

Ejemplo 2:
1,283333333333 ..... a Fracción
Llamemos x=1,283333333333 .....
1000x=1283,333333333 .....
100x=128,3333333333 .....
1000x-100x=900x=1283-128
x=1155/900

En palabras: Para convertir un Decimal Infinito Semiperiódico a Fracción, construyase una fracción:

Cuyo numerador sea la parte entera seguida de la parte decimal no periódica y seguida del periodo menos la parte entera seguida de la parte decimal no periódica

Y un denominador que tanga tantos nueves como dígitos tenga el periodo seguidos de tantos ceros como dígitos tenga la parte decimal no periódica:

1,283333333333 ..... = (1283 - 128) / (900)

Ecuaciones de la Recta

Desviación Media

La desviación media de un conjunto de datos es el promedio de la suma de los valores absolutos de las diferencias entre cada dato y el promedio del conjunto dado.

Cuadrado de Binomio

El cuadrado de un binomio es el cuadrado del primer término más o menos el doble producto del primero con el segundo más el cuadrado del segundo miembro.

Propiedades Raíces

Porcentaje

p % signifuca tomar p partes de un total de 100 partes. Esto se expresa por medio de la fracción:

p/100

El p% de una cantidad X se expresa del modo siguiente:

p% de X implica:

Nota: Entre Cantidades y sus porcentajes asociados

hay una relación de Directa Proporcionalidad.

Inversa Proporcionalidad

Variables Inversamente Proporcionales: Si x e y son dos variables inversamente proporcionales, entonces su relación queda representada por:

Donde k es la Constate de Proporcionalidad.

El gráfico correspondiente a esta relación es una curva llamada HIPERBOLA:

Número Intermedio

Pensemos que tenemos dos puntos de la recta Real, X1 y X2.

El Punto Intermedio, que equidsta de los dos puntos dados es:

Punto Medio = (X1 + X2) / 2

Rango de una Variable

Rango de una Variable: El rango de una variable es el conjunto de valores que puede tomar la variable. Por ejemplo: si H es la altura -medida en milímetros- del nivel de agua en un estanque de 1 metro de altura, el rango de H es el conjunto de todos los números reales entre 0 y 1000.

Número Racional

Número Racional: Todo número que se puede escribir como el cuociente de dos números enteros, con denominador no nulo.

Por ejemplo 0,45 es racional, porque se puede escribir como 45/100 = 9/20.

Pero Raíz de 2 NO es racional, porque no puede escribirse somo un cuociente de 2 números enteros. Por eso Raíz de 2 pertenece al conjunto de los Números Irracionales.

Volumen y Area Total de un Cubo

Volumen y Área Total Paralelepípedo

Area de Esfera - Volumen de Esfera

Función Parte Entera

La Función Parte Entera asocia a una número real el mayor de los números enteros que son menores o iguales a él.

Cuerda

Cuerda: Segmento de recta que une dos puntos en una circunferencia. El diámetro es un tipo especial de cuerda.

Cuadráticas Estudiadas en Currículum chileno de Media

Función Raiz Cuadrada - Cada rama UNA Función

Función Potencia

Función Potencia:

Una Función potencia está dada por la forma:

donde

a es un número Real Distinto de Cero.

y n = 2, 3, 4, 5 ....

Un poco de análisis de la Función Potencia: Vamos a comparar en gráfica (GRAPHMATICA) el comportamiento de x al cudrado y x a la cuarta, en los intervalos [0,1] y [1, +infinito[

Función Potencia Par e Impar:

Funciones Inversas

Grado de una Ecuación

Homotecia

Integral

Logaritmo en Base 2 - Grafo

Producto de Binomios con un Término en Común

Propiedades Logaritmos

Propiedad Fundamental Proporciones

Principal Axioma de Probabilidad

De donde viene esto?



Un evento "A" cualquiera debe cumplir que:

Entonces,

La probabilidad de un evento cualquiera es un número real entre 0 y 1, ambos inclusive.

Pendientes de la Recta - Posibles

Prueba de la Recta Vertical

Ejemplo Raíces de Ecuación Cuadrática

Raíz Cúbica de Producto - Raíz Cúbica de Cuociente

Raiz de Producto - Raíz de Cuociente

Recta por el Origen

Ejemplo de Región de Soluciones

Número Complejo

Representación Geométrica de Irracional

Rotación

ROTACION: Una rotación es una transformación que asocia a cada punto del plano una imagen de acuerdo a un punto llamado centro de rotación y a un ángulo que podemos llamar ángulo de giro.

Practicar una ROTACION:

Se escoge un punto O llamado centro de rotación. Con el compás, se toma la medida desde el centro, hacia el vértice A y con ese radio se traza un arco de circunferencia.Marcamos el vértice rotado A’.Para rotar los otros vértices debemos medir el ángulo que corresponde al arco dibujado con el vértice A y mantenerlo, para que la forma de la figura no cambie. Además debemos conservar el ángulo de giro. La figura obtenida es congruente con la primera.

Y ¿cómo se busca el centro de rotación? CENTRO de ROTACION: Se toma el punto medio entre A y A’ y se dibuja allí la simetral. Se toma el punto medio entre B y B’ y se dibuja allí la simetral. El punto de intersección es O.

Rotación en sistemas de Coordendas para ángulos especiales:Rotar (4,1) con centro de rotación O= (0,0), en 90°, 180°, 270°, 360°.

Las rotaciones requeridas serán:

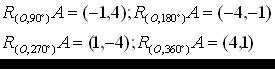Y Resumiendo:

Rotación en 180º